Trong không gian Oxyz, cho điểm A thỏa mãn OA → = 2 i → + j → là hai vectơ đơn vị trên hai trục tọa độ Ox, Oy. Tọa độ điểm A là:
A . A ( 2 ; 1 ; 0 )
B . A ( 0 ; 2 ; 1 )
C . A ( 0 ; 1 ; 1 )
D . A ( 1 ; 1 ; 1 )
Trong không gian tọa độ Oxyz, cho hai điểm A 1 ; - 2 ; - 2 ; B 2 ; 2 ; 1 . Tập hợp các điểm M thỏa mãn O M → ; O A → = O M → ; O B → là một mặt phẳng có phương trình
A. x + 4 y + 3 z = 0
B. 4 x - y + 3 z = 0
C. 3 x + 4 y + 3 z = 0
D. x - 4 y - 3 z = 0
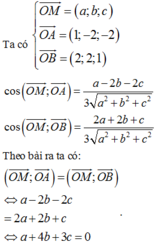
Vậy tập hợp các điểm M thỏa mãn yêu cầu bài toán thuộc mặt phẳng x + 4 y + 3 z = 0
Chọn A.
Trong không gian Oxyz, cho điểm A thỏa mãn ![]() . Khi đó tọa độ điểm A là:
. Khi đó tọa độ điểm A là:
A. (-2;3;7)
B. (2;-3;7)
C. (-3;2;7)
D. (2;7;-3).
Trong không gian Oxyz, cho a → =(-3;2;1) và điểm A(4;6;-3). Tìm tọa độ điểm B thỏa mãn .
A. (7;4;-4)
B. (1;8;-2)
C. (-7;-4;4)
D. (-1;-8;2)
Đáp án B
Phương pháp:
Hai vectơ
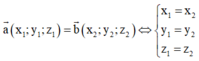
Cách giải:
Gọi điểm B x 0 ; y 0 ; z 0 là điểm cần tìm. Khi đó
![]()
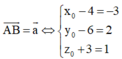
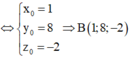
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-2; 2; -2); B(3; -3; 3). Điểm M trong không gian thỏa mãn MA/MB = 2/3. Khi đó độ dài OM lớn nhất bằng:
A. 6 3
B. 12 3
C. 5 3 2
D. 5 3
Chọn B
Gọi M (x; y; z)
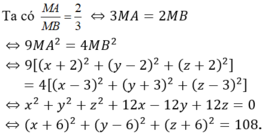
Như vậy, điểm M thuộc mặt cầu (S) tâm I(-6;6;-6) và bán kính R = √108 = 6√3. Do đó OM lớn nhất bằng
![]()
Trong không gian Oxyz, cho a → − 3 ; 2 ; 1 và điểm A 4 ; 6 ; − 3 . Tìm tọa độ điểm B thỏa mãn A B → = a → .
A. 7 ; 4 ; − 4
B. 1 ; 8 ; − 2
C. − 7 ; − 4 ; 4
D. − 1 ; − 8 ; 2
Trong không gian Oxyz, cho vecto a ⇀ ( - 3 ; 2 ; 1 ) và điểm A(4;6;-3). Tìm tọa độ điểm B thỏa mãn A B ⇀ = a ⇀
A. (7;4;-4)
B. (1;8;-2)
C. (-7;-4;4)
D. (-1;-8;2).
Trong không gian với hệ tọa độ O , i → , j → , k → cho 2 điểm A,B thỏa mãn O A → = 2 i → - j → + k → và O B → = i → + j → - 3 k → . Tìm tọa độ trung điểm M của đoạn thẳng AB
A. M 1 2 ; 0 ; - 1
B. M 3 2 ; 0 ; - 1
C. M(3;4;-2)
D. M 1 2 ; - 1 ; 2
Trong không gian với hệ tọa độ ( O , i ⇀ , j ⇀ , k ⇀ ) cho 2 điểm A,B thỏa mãn O A ⇀ = 2 i ⇀ - j ⇀ + k ⇀ và O B ⇀ = i ⇀ + j ⇀ - 3 k ⇀ . Tìm tọa độ trung điểm M của đoạn thẳng AB
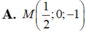
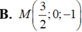
![]()
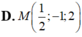
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;0;-3), B(-3;-2;-5). Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức AM2 + BM2 = 30 là một mặt cầu (S). Tọa độ tâm I và bán kính R của mặt cầu (S) là:
A . I - 2 ; - 2 ; - 8 ; R = 3
B . I ( - 1 ; - 1 ; - 4 ) ; R = 6
C . I ( - 1 ; - 1 ; - 4 ) ; R = 3
D . I ( - 1 ; - 1 ; - 4 ) ; R = 30 2
Chọn C
Gọi tọa độ điểm M(x;y;z)
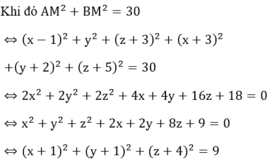
là phương trình của mặt cầu (S), có tâm I (-1;-1;-4) và bán kính R = 3