Đường thẳng qua hai cực trị của hàm số f ( x ) = x 2 - x + 2 1 + x song song với
A. 2x + y - 1 =0
B. x - 2y - 1 = 0
C. 2x - y - 3 = 0
D. x + 2y - 3 = 0
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số f ( x ) = - 2 x 3 + 3 x 2 + 1
![]()
![]()
![]()
![]()
Đường thẳng qua hai cực trị của hàm số f x = x 2 - x + 2 1 + x song song với
A. 2x + y - 1 = 0
B. x - 2y - 1 = 0
C. 2x - y - 3 = 0
D. x + 2y - 3 = 0
Cho hàm số y= x3-3x2-mx+2 với m là tham số thực. Tìm giá trị của m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số tạo với đường thẳng d ; x+4y-5=0 một góc α = 45 ° .
A. m= -1/2
B. m= 1/2
C. m=0
D. m= 1
Ta có y’=3x2-6x-m
Để đồ thị hàm số đã cho có hai điểm cực trị khi phương trình y’=0 có hai nghiệm phân biệt ⇔ ∆ ' = 9 + 3 m > 0 ⇔ m > - 3
Ta có 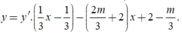
đường thẳng đi qua hai điểm cực trị Avà B là 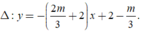
Đường thẳng d; x+4y-5=0 có một VTPT là n d → = ( 1 ; 4 ) .
Đường thẳng 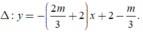 có một VTCP là
n
∆
→
=
(
2
m
3
+
2
;
1
)
có một VTCP là
n
∆
→
=
(
2
m
3
+
2
;
1
)
Ycbt suy ra:
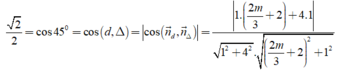
Suy ra
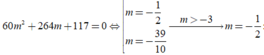 thỏa mãn
thỏa mãn
Chọn A.
Cho hàm số y = 2 x 3 - 3 m 2 - m + 1 x 2 + 6 m 2 - 6 m x , với m là tham số. Gọi S là tập hợp các giá trị của m để đồ thị hàm số đã cho có hai điểm cực trị, đồng thời đường thẳng đi qua hai điểm cực trị đó vuông góc với đường thẳng y = x + 2 . Số phần tử của tập hợp S là
A. 2
B. 3
C. 1
D. 4
Chọn đáp án D
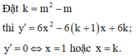
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi k ≠ 1
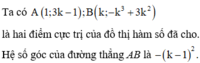
Đường thẳng AB vuông góc với đường thẳng y = x + 2 khi và chỉ khi

Cho hàm số y=f(x) có đạo hàm xác định và liên tục trên Rvới y = f ' ( x ) = x 3 - x 2 - 2 x . Gọi k là hệ số góc của đường thẳng đi qua hai điểm cực tiểu của đồ thị hàm số y=f(x). Khẳng định nào sau đây đúng ?
![]()
![]()
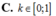

Cho hàm số y=f(x) có bảng biến thiên như hình bên dưới.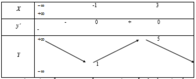
Phương trình đường thẳng đi qua hai điểm cực đại và cực tiểu của đồ thị hàm số đã cho là
![]()
![]()
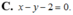
![]()
Giá trị m để đường thẳng đi qua hai điểm cực trị của hàm số y = x 3 + m x 2 - ( m - 1 ) x - m 2 là đường thẳng 2x+3y=0 là:
A. m=0
B. m=1
C. m=2
D. m=3
Giả sử đồ thị hàm số y=x3 -3mx2+3(m+6)x+1 có hai cực trị. khi đó đường thẳng qua hai điểm cực trị có phương trình là:
Giả sử đồ thị hàm số y=x3 -3mx2+3(m+6)x+1 có hai cực trị. khi đó đường thẳng qua hai điểm cực trị có phương trình là: