Cho các hàm số f x = x 4 + 2018 , g x = 2 x 3 - 2018 và h x = 2 x - 1 x + 1 . Trong các hàm số đã cho, có tất cả bao nhiêu hàm số không có khoảng nghịch biến?
A. 2
B. 1
C. 0
D. 3
Cho các hàm số f(x) = x4 + 2018, g(x)= 2x3 - 2018 và h ( x ) = 2 x - 1 x + 1 . Trong các hàm số đã cho, có tất cả bao nhiêu hàm số không có khoảng nghịch biến?
A. 2
B. 1
C. 0
D. 3
Cho các hàm số f ( x ) = x 4 + 2018 ; g ( x ) = 2 x 3 - 2018 v à h ( x ) = 2 x - 1 x + 1 . Trong các hàm số đã cho, có tất cả bao nhiêu hàm số không có khoảng nghịch biến?
A. 2
B. 1
C. 0
D. 3
Đáp án là A
![]() nên hàm số có khoảng đồng biến và nghịch biến.
nên hàm số có khoảng đồng biến và nghịch biến.
![]() nên hàm số luôn đồng biến trên R.
nên hàm số luôn đồng biến trên R.
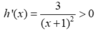 nên hàm số luôn đồng biến trên từng khoảng xác định.
nên hàm số luôn đồng biến trên từng khoảng xác định.
Vậy có 2 hàm số không có khoảng nghịch biến.
Cho hàm số y = f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) = (1–x)(x+2)g(x)+2018 với g(x) < 0, ∀ x ∈ R . Hàm số y = f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞
Đáp án D
Ta có Đáp án D
Ta có y’ = –f’(1 – x) + 2018 = –[1–(1–x)][(1–x)+2]g(1–x) – 2018 + 2018
= –x(3–x)g(1–x)
Suy ra 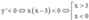 (vì g(1–x) < 0,
∀
x
∈
R
)
(vì g(1–x) < 0,
∀
x
∈
R
)
Vậy hàm số đã cho nghịch biến trên khoảng 3 ; + ∞
Cho hàm số y=f(x) xác định trên R và có đạo hàm f‘(x) thỏa mãn f’(x)=(1-x)(x+2).g(x) + 2018 trong đó g(x)<0, mọi x thuộc R. Hàm số y=f(1-x)+2018x+2019 nghịch biến trên khoảng nào?
![]()
![]()
![]()
![]()
Cho hàm số f(x) xác định và liên tục trên R và có đạo hàm f'(x) thỏa mãn f ' ( x ) = ( 1 - x ) ( x + 2 ) g ( x ) + 2018 với g ( x ) < 0 , ∀ x ∈ R . Hàm số y = f ( 1 - x ) + 2018 x + 2019 nghịch biến trên khoảng nào dưới đây?
A . ( 1 ; + ∞ ) .
B . ( 0 ; 3 ) .
C . ( - ∞ ; 3 ) .
D . ( 4 ; + ∞ ) .
Cho hàm số y=f(x) liên tục trên R có đạo hàm cấp 3 với f’’’(x)=0 và thỏa mãn f ( x ) ' 2018 1 - f ' ' ( x ) = 2 x ( x + 1 ) 2 ( x - 2018 ) 2019 : f ' ' ( x ) , ∀ x ∈ R Hàm số g ( x ) = f ' ( x ) 2019 1 - f ' ' ( x ) có bao nhiêu điểm cực trị?
A. 1
B.2
C.3
D. 4
Cho hàm số y = f(x) xác định trên R. Đồ thị hàm số y = f’(x) như hình vẽ bên. Đặt g ( x ) = f ( x ) - 1 3 x 3 - 3 4 x 2 + 3 2 x + 2018 . Điểm cực tiểu của hàm số g(x) đoạn [–3;1] là:
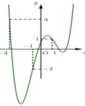
A. x C T = - 1
B. x C T = 1 2
C. x C T = - 2
D. x C T = 0
Đáp án A.
Phương pháp: Tính g’(x) tìm các nghiệm của phương trình g’(x) = 0
Điểm x0 được gọi là điểm cực tiểu của hàm số y = g(x) khi và chỉ khi g’(x0) = 0 và qua điểm x = x0 thì g’(x) đổi dấu từ âm sang dương.
Cách giải:
![]()
![]()
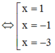
Khi x<1 ta có: 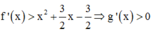
Khi x>1 ta có: 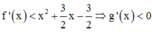
Qua x = 1, g’(x) đổi dấu từ dương sang âm => x = 1 là điểm cực đại của đồ thị hàm số y = g(x)
Chứng minh tương tự ta được x = –1 là điểm cực tiểu và x = –3 là điểm cực đại của đồ thị hàm số y = g(x)
Cho hàm số y=f(x)>0 xác định và có đạo hàm trên đoạn [0;1] và thỏa mãn các điều kiện sau: g(x)=1+2018 ∫ 0 x f ( t ) dt ; g ( x ) = f 2 ( x ) . Tính ∫ 0 1 ( g ( x ) dx ?
A. 1011/2.
B. 1009/2.
C. 2019/2.
D. 505
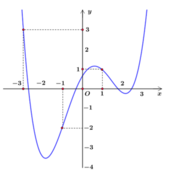
Cho hàm số y = f(x). Đồ thị hàm số đạo hàm y = f'(x) như hình vẽ dưới đây. Xét hàm số g(x) = f(x) - 1 3 x 3 - 3 4 x 2 + 3 2 x + 2018 . Mệnh đề nào dưới đây đúng?
A. m i n [ - 3 ; 1 ] g ( x ) = g(1)
B. m i n [ - 3 ; 1 ] g ( x ) = g(-3)
C. m i n [ - 3 ; 1 ] g ( x ) = g ( - 3 ) + g ( 1 ) 2
D. m i n [ - 3 ; 1 ] g ( x ) = g(-1)
Chọn D
Xét hàm số g(x) = f(x) - 1 3 x 3 - 3 4 x 2 + 3 2 x + 2018 .
![]()
Cho ![]()
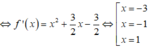
Dựa vào đồ thị ta so sánh được m i n [ - 3 ; 1 ] g ( x ) = g(-1)
Cho hàm số y = f(x). Đồ thị hàm số đạo hàm y = f'(x) như hình vẽ dưới đây. Xét hàm số g(x) = f(x) - 1 3 x 3 - 3 4 x 2 + 3 2 x + 2018 . Mệnh đề nào dưới đây đúng?
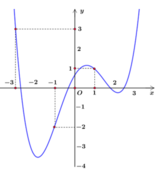
A. m i n [ - 3 ; 1 ] g ( x ) = g(1)
B. m i n [ - 3 ; 1 ] g ( x ) = g(-3)
C. m i n [ - 3 ; 1 ] g ( x ) = g ( - 3 ) + g ( 1 ) 2
D. m i n [ - 3 ; 1 ] g ( x ) = g(-1)
Chọn D
Cho hàm số y = f(x). Đồ thị hàm số đạo hàm y = f'(x) như hình vẽ dưới đây. Xét hàm số
![]()
![]()
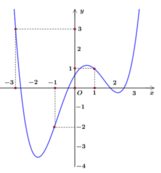
Cho ![]()
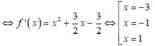
Dựa vào đồ thị ta so sánh được ![]()