Thể tích của chóp tam giác đều có tất cả các cạnh đều bằng a là
A. a 3 2 4
B. a 3 2 2
C. a 3 2 6
D. a 3 2 12
Thể tích khối chóp tam giác đều có tất cả các cạnh bằng a
A. a 3 2 4
B. a 3 2 6
C. a 3 2 12
D. a 3 3 12
Đáp án C
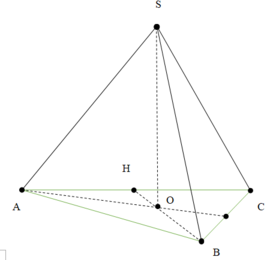
Gọi O là trọng tâm ∆ABC
Kẻ BH AC
Vì SABC là tứ diện đều => SO ⊥ (ABC)
Vì ∆ABC đều => BO = 2 3 BH = a 3 3
Xét ∆SBO vuông tại O
S O 2 + O B 2 = S B 2
-> SO= a 6 3
V S . A B C = 1 3 ⋅ a 6 3 ⋅ a 2 ⋅ 1 2 ⋅ sin A = a 2 12
Thể tích khối chóp tam giác đều có tất cả các cạnh bằng a
A . a 3 2 4
B . a 3 2 6
C . a 3 2 12
D . a 3 3 12
Đáp án C
Gọi O là trọng tâm ∆ABC
Kẻ BH ⊥ AC
Vì SABC là tứ diện đều => SO ⊥ (ABC)
Vì ∆ABC đều => BO = 2 3 BH = a 3 3
Xét ∆SBO vuông tại O

= a 3 12 2
Cho khối lăng trụ tam giác đều A B C . A 1 B 1 C 1 có tất cả các cạnh bằng a. Gọi M là trung điểm của A A 1 . Thể tích khối chóp M . B C A 1 là:

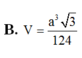
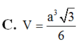
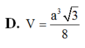
Cho khối lăng trụ tam giác đều ABC. A 1 B 1 C 1 có tất cả các cạnh bằng a. Gọi M là trung điểm của AA 1 . Thể tích khối chóp M . BCA 1 là:
A. V = a 3 3 12
B. V = a 3 3 24
C. V = a 3 3 6
D. V = a 3 3 8
Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a là
A. a 3 2 3
B. a 3 3 3
C. a 3 2 6
D. a 3 2 2
Chọn C.
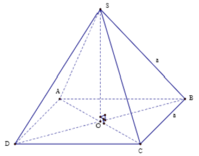
Gọi khối chóp tứ giác đều là S.ABCD
Gọi O là tâm của đáy Do là khối chóp tứ giác đều nên SO ⊥ (ABCD)
Vậy SO là chiều cao của khối chóp S.ABCD.
Xét tam giác vuông SOB, ta có:
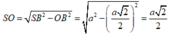
Thể tích khối chóp là:
![]()
Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a là
A. a 3 2 3
B. a 3 3 3
C. a 3 2 6
D. a 3 2 2
Thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a là
A. 2 a 3 3
B. 3 a 3 3
C. 2 a 3 6
D. 2 a 3 2
Đáp án là C
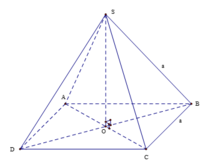
Gọi khối chóp tứ giác đều là S.ABCD
Gọi O là tâm của đáy ABCD. Do S.ABCD là khối chóp tứ giác đều nên SO ⊥ (ABCD)
Vậy SO là chiều cao của khối chóp S.ABCD.
Xét tam giác vuông SOB, ta có
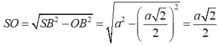
Thể tích của khối chóp S.ABCD là
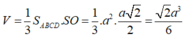
Cho khối lăng trụ tam giác đều ABC. A 1 B 1 C 1 có tất cả các cạnh bằng a. Gọi M là trung điểm của AA 1 . Thể tích khối chóp M.BC A 1 là:
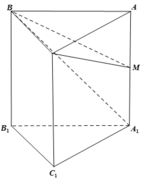
A. a 3 3 12
B. a 3 3 24
C. a 3 3 6
D. a 3 3 8
Cho (H) là khối chóp tứ giác đều có tất cả các cạnh bằng a. Tính thể tích của (H).
A. a 3 3 2
B. a 3 3 4
C. a 3 3
D. a 3 2 6
Đáp án D
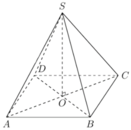
Gọi khối chóp tứ giác đều đó là S. ABCD.
Gọi O là giao điểm hai đường chéo hình vuông ABCD, ta có SO là đường cao hình chóp.
S O = S A 2 - A O 2 = a 2 - a 2 2 2 = a 2 2
S A B C D = a 2
Vậy thể tích cần tìm là:
V = 1 3 . S A B C D . S O = 1 3 a 2 . a 2 2 = a 3 2 6