Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên
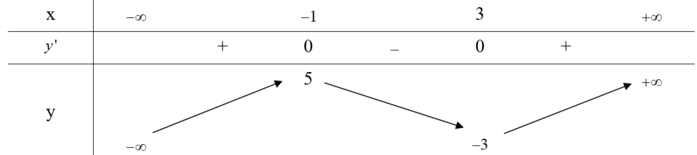
Phương trình f 1 − 2 x + 2 = 5 có tất cả bao nhiêu nghiệm thực phân biệt
A. 5
B. 4
C. 3
D. 6
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên
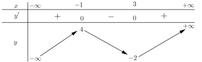
Số nghiệm của phương trình |f(x)|=2 là
A. 3.
B. 6.
C. 4.
D. 5.
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên:

Số nghiệm của phương trình f(x) - 2=0 là:
A. 1.
B. 2.
C. 0.
D. 3.
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên: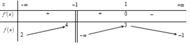
Số nghiệm của phương trình f(x) - 2 = 0 là:
![]()
![]()
![]()
![]()
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ bên:
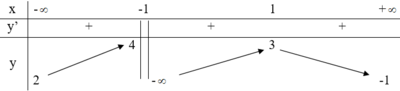
Số nghiệm của phương trình f(x) – 2 = 0 là:
A. 0
B. 1
C. 3
D. 2
Đáp án D.
Phương pháp: Số nghiệm của phương trình f(x) = m là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m
Cách giải: f(x) – 2 = 0 → f(x) = 2
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = 2
Dựa vào BBT ta thấy phương trình có 2 nghiệm
Cho hàm số y = f (x) có bảng biến thiên như hình vẽ bên. Số nghiệm của phương trình f x − 1 = 2 là:
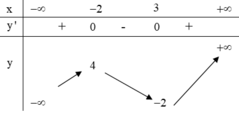
A. 5
B. 4
C. 2
D. 3
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ.
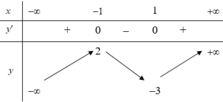
Số nghiệm của phương trình f(x) + 3 = 0là
A. 0
B. 3
C. 2
D. 1
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên
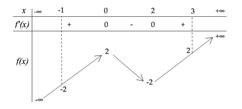
Có bao nhiêu số nguyên dương m để phương trình f(2 sinx+1)=f(m) có nghiệm thực ?
A. 2.
B. 5.
C. 4.
D. 3.
Cho hàm số y = f(x). Hàm số y = f '(x) có bảng biến thiên như hình vẽ:
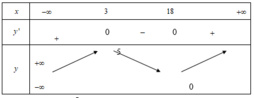
Bất phương trình e x ≥ m - f ( x ) có nghiệm x ∈ 4 ; 16 khi và chỉ khi
A. m ≤ f ( 4 ) + e 2
B. m < f ( 4 ) + e 2
C. m ≤ f ( 16 ) + e 4
D. m < f ( 16 ) + e 4
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ bên và f(-2) = 3. Tập nghiệm của bất phương trình f(x) > 3 là
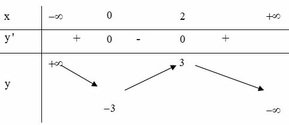
A. S = - 2 ; 2
B. S = - ∞ ; - 2
C. S = - ∞ ; - 2 ∪ 2 ; + ∞
D. S = - 2 ; + ∞
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên:
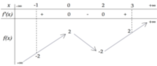
Có bao nhiêu số nguyên dương m để phương trình f 2 sin x + 1 = f ( m )
A. 2
B. 5
C. 4
D. 3