CMR:Nếu a2 =bc thì :
(a + b)/(a-b)=(c+a)/(c-a)
Cho a+1/b=b+1/c =c+1/a
a,Cho a =1,tìm b,c
b,cmr:nếu a,b,c đôi 1 khác nhau thì a^2.b^2.c^2=1
c,cmr:nếu a,b,c>0thif a=b=c
CMR:nếu a/b=c/d thì a+c/d+b = a/b
CMR:Nếu \(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}\)thì a=b=c
Áp dụng tc của dãy tỉ số bằng nhau ta có :
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{a+b+c}=1\)
=> a/b = 1 => a = b ( 1 )
=> b/c = 1 => b = c ( 2 )
=> a/c = 1 => a = c ( 3 )
Từ (1)(2)(3) => đpcm
Áp dụng t/c dãy tỉ số bằng nhau :
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{b+c+a}=1\)
\(\Rightarrow a=1.b=b\)
\(b=1.c=c\)
\(\Rightarrow a=b=c\)( ĐPCM )
Ta có : \(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{b+c+a}=1\)
\(\Leftrightarrow\hept{\begin{cases}\frac{a}{b}=1\\\frac{b}{c}=1\\\frac{c}{a}=1\end{cases}\Leftrightarrow\hept{\begin{cases}a=b\\b=c\\c=a\end{cases}\Leftrightarrow}a=b=c}\)
Vậy _
Cho P=(a+b+c)(ab+bc+ca)+abc
a)Phân tích P thành nhân tử
b)Cmr:Nếu a,b,c là các số nguyên mà a+b+c chia hết cho 6 thì P- 4abc cũng chia hết cho 6
Chứng minh rằng:
Nếu a2 = bc (với a ≠ b và a ≠ c) thì a + b a - b = c + a c - a
Ta có:
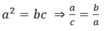
Theo tính chất dãy tỉ số bằng nhau ta có:
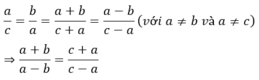
CMR:Nếu a.b=c^2(a,b,c thuộc N*) và ƯCLN(a,b)=1 thì a và b đều là các số chính phương
CMR:Nếu a>b>c thì \(\frac{2a^2}{a-b}+\frac{b^2}{b-c}>2a+3b+c\)
CMR:nếu a^2+b^2=c^2+d^2 thì a+b+c+d là hợp số hay số nguyên tố
Ta có: \(a\left(a-1\right)+b\left(b-1\right)+c\left(c-1\right)+d\left(d-1\right)⋮2\)(tích 2 số nguyên liên tiếp)
\(\Leftrightarrow\left(a^2+b^2+c^2+d^2\right)-\left(a+b+c+d\right)⋮2\)
Mà \(a^2+b^2=c^2+d^2\)
\(\Rightarrow2\left(a^2+b^2\right)-\left(a+b+c+d\right)⋮2\)
\(\Rightarrow a+b+c+d⋮2\)
Mà a, b, c, d nguyên dương => a+ b+ c+ d > 2
=> a+ b+ c+ d là hợp số
Bổ sung \(a;b;c;d\in Z^+\)
Xét \(\left(a^2+b^2+c^2+d^2\right)-\left(a+b+c+d\right)\)
\(=\left(a^2-a\right)+\left(b^2-b\right)+\left(c^2-c\right)+\left(d^2-d\right)\)
\(=a\left(a-1\right)+b\left(b-1\right)+c\left(c-1\right)+d\left(d-1\right)\)
Lạp luận tích 2 số nguyên liên tiếp chia hết cho 2
\(\Rightarrow\left(a^2+b^2+c^2+d^2\right)-\left(a+b+c+d\right)⋮2\) \(\left(1\right)\)
Lại có: \(a^2+b^2=c^2+d^2\)
\(\Rightarrow a^2+b^2+c^2+d^2=2\left(b^2+a^2\right)\)
\(\Rightarrow a^2+b^2+c^2+d^2⋮2\) \(\left(2\right)\)
Từ (1) và (2) suy ra
\(a+b+c+d⋮2\)
Mà \(a+b+c+d>2\) \(Do\)\(a;b;c;d\in Z^+\)
\(\Rightarrow a+b+c+d\)là hợp số
Đề phải cho a,b,c,d thuộc N sao chứ bạn ơi
Có : a^2+b^2+c^2+d^2
=> 2.(a^2+b^2) = a^2+b^2+c^2+d^2
=> a^2+b^2+c^2+d^2 chia hết cho 2
Xét :a^2-a = a.(a-1)
Ta thấy a-1;a là 2 số tự nhiên liên tiếp => có 1 số chia hết cho 2
=> (a-1).a chia hết cho 2 hay a^2-a chia hết cho 2
Tương tự : b^2-b ; c^2-c ; d^2-d đều chia hết cho 2
=> (a^2+b^2+c^2+d^2)-(a+b+c+d) chia hết cho 2
Mà a^2+b^2+c^2+d^2 chia hết cho 2 => a+b+c+d chia hết cho 2
Mặt khác : a,b,c,d thuộc N sao nên a+b+c+d > 2
=> a+b+c+d là hợp số
Tk mk nha
1, CMR:nếu a/b=b/c=c/a thì a=b=c
2,Tìm x,y,z biết x/3=y/6=z/10 và x+z=7+y
1)
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{b+C+a}=1\)
=> a=b ; b=c => a=b=c
=> đpcm
2)
\(\frac{x}{3}=\frac{y}{6}=\frac{z}{10}=\frac{x+z}{3+10}=\frac{7+y}{13}\)
=> 13y = 6.(7+y)
=> 13y = 42+6y
=> 7y = 42
=> y=6
=> x/3 = z/10 = 1
=> x=3 ; y=10