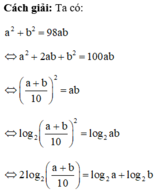Cho a,b là các số thực dương thỏa mãn a 2 + b 2 = 14 a b . Khẳng định nào sau đây sai?
A. 2 log 2 a + b = 4 + log 2 a + log 2 b .
B. ln a + b 4 = ln a + ln b 2 .
C. 2 log a + b 4 = log a + log b .
D. 2 log 4 a + b = 4 + log 4 a + log 4 b .
Những câu hỏi liên quan
Cho 2 số thực dương a,b thỏa mãn 1 a b 0 Khẳng định nào sau đây là đúng A. logab 1 logba B. 1 logab log ba C. logab logba 1 D. logba 1 logab
Đọc tiếp
Cho 2 số thực dương a,b thỏa mãn 1> a> b> 0 Khẳng định nào sau đây là đúng
A. logab< 1< logba
B. 1< logab< log ba
C. logab< logba< 1
D. logba< 1< logab
Chọn D
Cho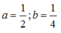 
ta thấy logab= 2 và logba= ½. Do vậy logba< 1< logab
Đúng 0
Bình luận (0)
Cho 2 số thực dương a và b thỏa mãn 1 a b. Khẳng định nào sau đây là đúng. A. logab 1 logba B. 1 logab logba C. logab logba 1 D. logba 1 logab
Đọc tiếp
Cho 2 số thực dương a và b thỏa mãn 1< a< b. Khẳng định nào sau đây là đúng.
A. logab< 1< logba
B. 1< logab< logba
C. logab< logba< 1
D. logba< 1< logab
Chọn D
Cách 1: Cho a= 4; b= 2 ta thấy log24> 1> log42
Cách 2: Ta có: 1< a< b nên
Đúng 0
Bình luận (0)
Cho a,b là các số thực dương thỏa mãn
a
2
+
b
2
14
a
b
.
Khẳng định nào sau đây sai? A.
2
log
2
a
+
b
4
+
log
2
a
+
log...
Đọc tiếp
Cho a,b là các số thực dương thỏa mãn a 2 + b 2 = 14 a b . Khẳng định nào sau đây sai?
A. 2 log 2 a + b = 4 + log 2 a + log 2 b .
B. 2 log a + b 4 = log a + log b .
C. ln a + b 4 = ln a + ln b 2 .
D. 2 log 2 a + b = 4 + log 4 a + log 4 b .
Cho a, b là các số thực dương thỏa mãn log 2 a + log 2 b = 0. Khẳng định nào sau đây đúng?
A. a + b = 2
B. a + b = 1
C. ab=1
D. ab=2
Cho các số thực dương a,b thỏa mãn
a
2
3
a
3
5
và
log
b
2
3
log
b
3
5
. Khẳng định nào sau đây là đúng? A.
0
log
a
b...
Đọc tiếp
Cho các số thực dương a,b thỏa mãn a 2 3 > a 3 5 và log b 2 3 < log b 3 5 . Khẳng định nào sau đây là đúng?
A. 0 < log a b < 1.
B. log a b > 1.
C. log b a < 0.
D. 0 < log b a < 1.
Cho các số thực dương a,b thỏa mãn
a
2
3
a
3
5
và
log
b
2
3
log
b
3
5
. Khẳng định nào sau đây là đúng? A.
0
log
a
b...
Đọc tiếp
Cho các số thực dương a,b thỏa mãn a 2 3 > a 3 5 và log b 2 3 < log b 3 5 . Khẳng định nào sau đây là đúng?
A. 0 < log a b < 1.
B. log a b > 1.
C. log b a < 0.
D. 0 < log b a < 1.
Đáp án C
Cách 1: Tư duy tự luận
Ta có a 2 3 > a 3 5 2 3 > 3 5 ⇒ a > 1 và log b 2 3 < log b 3 5 . 2 3 > 3 5 ⇒ 0 < b < 1. Vậy log a b < 0 log b a < 0
Cách 2: Sử dụng máy tính cầm tay
Chọn các giá trị
a = 0,5 ∈ 0 ; 1 ; a = 1,5 ∈ ( 1 ; + ∞ ) ; b = 0,3 ∈ ( 0 ; 1 ) ; b = 1,3 ∈ ( 1 ; + ∞ )
Ta chọn được các giá trị a =1,5 và b = 0,3 thỏa mãn điều kiện.
Ấn tiếp
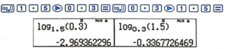
Vậy log a B < 0 và log b a < 0.
Đúng 0
Bình luận (0)
Cho các số thực a, b, thỏa mãn a - b = 2 . Khẳng định nào sau đây là đúng?
Tích của hai số a và b:
A. có giá trị nhỏ nhất là -1
B. có giá trị lớn nhất là -1
C. có giá trị nhỏ nhất khi a = b
D. không có giá trị nhỏ nhất
Ta có: a – b = 2 nên a= b +2.
Khi đó; tích a b = b + 2 . b = b 2 + 2 b = b 2 + 2 b + 1 - 1 = b + 1 2 - 1 ≥ - 1 ∀ b
Vậy tích ab nhỏ nhất là -1 khi b = -1 ; a= 1
Đúng 0
Bình luận (0)
Cho các số thực dương x; y thỏa mãn x2 + y2 14. Khẳng định nào sau đây là đúng ? A.
log
2
x
+
y
14
log
2
x+
log
2
y B.
log
2
x
+
y...
Đọc tiếp
Cho các số thực dương x; y thỏa mãn x2 + y2 = 14. Khẳng định nào sau đây là đúng ?
A. log 2 x + y 14 = log 2 x+ log 2 y
B. log 2 x + y 16 =x+ log 2 y
C. log 2 ( x + y ) = log 2 x + log 2 y 2
D. log 2 x + y = 2 + log 2 x y 2
Chọn D.
Ta có: x2 + y2 = 14. Nên (x + y)2 = 16xy
Suy ra: log2(x + y) 2 = log2( 16xy)
Đúng 0
Bình luận (0)
Cho hai số thực dương a và b thỏa mãn
a
2
+
b
2
98
a
b
. Khẳng định nào sau đây đúng ? A.
2
log
2
a
+
b
log
2
a
+
log
2
b
B.
log...
Đọc tiếp
Cho hai số thực dương a và b thỏa mãn a 2 + b 2 = 98 a b . Khẳng định nào sau đây đúng ?
A. 2 log 2 a + b = log 2 a + log 2 b
B. log 2 a + b 2 = log 2 a + log 2 b
C. 2 log 2 a + b 10 = log 2 a + log 2 b
D. log 2 a + b 10 = 2 log 2 a + log 2 b
Chọn C.
Phương pháp: Để làm tốt dạng toán này chúng ta cần quan sát 4 đáp án xem có đặc điểm gì chung. Từ đó tìm ra phép biến đổi phù hợp.
Đúng 0
Bình luận (0)