Cho f x = x 4 - 5 x 2 + 4 . Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị hàm số y = f(x) và trục hoành. Mệnh đề nào sau đây sai?
A. S = ∫ - 2 2 f x d x
B. S = 2 ∫ 0 1 f x d x + 2 ∫ 1 2 f x d x
C. S = ∫ 0 2 f x d x
D. S = 2 ∫ 0 2 f x d x
Những câu hỏi liên quan
Cho hàm số yf(x) liên tuc trên R và thỏa mãn f(0)0f(-1) Gọi S là diện tích hình phẳng giới hạn bởi các đường
y
f
x
,
y
0
,
x
−
1
v
à
x
1.
Xét các mênh đề sau
1.
S
∫
−
1...
Đọc tiếp
Cho hàm số y=f(x) liên tuc trên R và thỏa mãn f(0)<0<f(-1) Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f x , y = 0 , x = − 1 v à x = 1. Xét các mênh đề sau
1. S = ∫ − 1 0 f x d x + ∫ 0 1 f x d x 2. S = ∫ − 1 1 f x d x 3. S = ∫ − 1 1 f x d x 4. S = ∫ − 1 1 f x d x
Số mệnh đề đúng là
A. 2
B. 1
C. 3
D. 4
Đáp án B
Do f 0 < 0 < f − 1 nên phương trình f x = 0 có ít nhất 1 nghiệm x ∈ − 1 ; 0
Đáp án đúng là S = ∫ − 1 1 f x d x
Đúng 0
Bình luận (0)
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y f(x), trục hoành, đường thẳng x a, x b ( như hình bên). Biết
∫
a
c
f
(
x
)
d
x
-
2
và
∫
c
b
f
(
x
)
d
x
5
. Hỏi S bằng bao nhiêu? A. 7 B....
Đọc tiếp
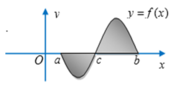
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành, đường thẳng x = a, x = b ( như hình bên). Biết ∫ a c f ( x ) d x = - 2 và ∫ c b f ( x ) d x = 5 . Hỏi S bằng bao nhiêu?
A. 7
B. 5
C. 2
D.3
Cho các Parabol có các đỉnh lần lượt là I1, I2. Gọi A, B là giao điểm của (P1) và Ox. Biết rằng 4 điểm A, B, I1, I2 tạo thành tứ giác lồi có diện tích bằng 10. Tính diện tích S của tam giác IAB với I là đỉnh của Parabol (P): y h(x) f(x) + g(x). (P1): y f(x)
1
4
x
2
-
x
, P(2): y g(x)
a
x
2
-
4
a
x
+
b...
Đọc tiếp
Cho các Parabol có các đỉnh lần lượt là I1, I2. Gọi A, B là giao điểm của (P1) và Ox. Biết rằng 4 điểm A, B, I1, I2 tạo thành tứ giác lồi có diện tích bằng 10. Tính diện tích S của tam giác IAB với I là đỉnh của Parabol (P):
y = h(x) = f(x) + g(x). (P1): y = f(x) = 1 4 x 2 - x , P(2): y = g(x) = a x 2 - 4 a x + b (a>0)
A. S = 6.
B. S = 4.
C. S = 9.
D. S = 7.
Chọn A.
(P1): y = f(x) = 1 4 x 2 - x có đỉnh I 2 (2;-1)
P(2): y = g(x) =
a
x
2
-
4
a
x
+
b
(a>0) 
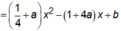
Duy ra I1, I2, I cùng nằm trên đường thẳng x = 2.
Mà giao điểm của (P1) và Ox là A(4;0) và B(0;0).
Suy ra tứ giác lồi AI1BI2 có hai đường chéo vuông góc và b – 4a >0
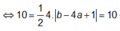
Tam giác IAB có diện tích là
Đúng 0
Bình luận (0)
Biết đồ thị hàm số
f
(
x
)
a
x
4
+
b
x
2
+
c
cắt trục hoành tại 4 điểm phân biệt. Gọi
S...
Đọc tiếp
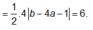
Biết đồ thị hàm số f ( x ) = a x 4 + b x 2 + c cắt trục hoành tại 4 điểm phân biệt. Gọi S 1 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f ( x ) nằm dưới trục hoành. Gọi S 2 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f ( x ) nằm phía trên trục hoành. Cho biết 5 b 2 = 36 a c . Tính tỉ số S 1 S 2
A. S 1 S 2 = 2 .
B. S 1 S 2 = 1 4 .
C. S 1 S 2 = 1 2 .
D. S 1 S 2 = 1 .
Đáp án D
Phương trình hoành độ giao điểm của đồ thị f ( x ) và Ox: a x 4 + b x 2 + c = 0 .
Để phương trình có bốn nghiệm
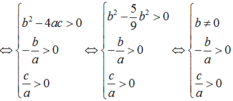
Gọi x 1 , x 2 , x 3 , x 4 lần lượt là bốn nghiệm của phương trình a x 4 + b x 2 + c = 0 và x 1 < x 2 < x 3 < x 4 . Không mất tính tổng quát, giả sử a > 0 .
Khi đó
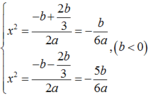
Suy ra x 1 = - - 5 b 6 a ; x 2 = - - b 6 a ; x 3 = - b 6 a ; x 4 = - b 6 a .
Do đồ thị hàm số f ( x ) nhận trục tung làm trục đối xứng nên ta có:
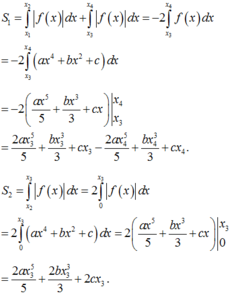
Suy ra
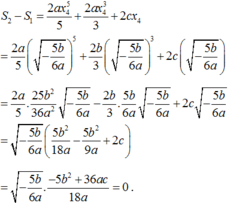
Vậy S 1 = S 2 hay S 1 S 2 = 1 .
Đúng 0
Bình luận (0)
Cho hình phẳng D giới hạn bởi đồ thị của hai hàm số yf(x),yg(x) (phần tô màu như hình vẽ). Gọi S là diện tích hình phẳng D. Mệnh đề nào dưới đây đúng? A.
S
∫
-
3
0
[
f
(
x
)
-
g
(
x
)
]
dx
.
B.
S
∫...
Đọc tiếp
Cho hình phẳng D giới hạn bởi đồ thị của hai hàm số y=f(x),y=g(x) (phần tô màu như hình vẽ). Gọi S là diện tích hình phẳng D. Mệnh đề nào dưới đây đúng?
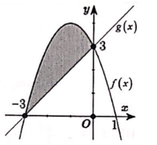
A. S = ∫ - 3 0 [ f ( x ) - g ( x ) ] dx .
B. S = ∫ - 3 0 [ g ( x ) - f ( x ) ] dx .
C. S = ∫ - 3 0 [ f ( x ) + g ( x ) ] dx .
D. S = ∫ - 3 1 [ f ( x ) - g ( x ) ] 2 dx .
Biết đồ thị hàm số
f
x
a
x
4
+
b
x
2
+
c
cắt trục hoành tại 4 điểm phân biệt. Gọi
S
1
là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm dưới trục hoành. Gọi
S
2
là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm...
Đọc tiếp
Biết đồ thị hàm số f x = a x 4 + b x 2 + c cắt trục hoành tại 4 điểm phân biệt. Gọi S 1 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm dưới trục hoành. Gọi S 2 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm phía trên trục hoành. Cho biết 5 b 2 = 36 a c . Tính tỉ số S 1 S 2
A. S 1 S 2 = 2
B. S 1 S 2 = 1 4
C. S 1 S 2 = 1 2
D. S 1 S 2 = 1
Biết đồ thị hàm số
f
x
a
x
4
+
b
x
2
+
c
cắt trục hoành tại 4 điểm phân biệt. Gọi
S
1
là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm dưới trục hoành. Gọi
S
2
là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm phía trên trục hoành. Cho biết...
Đọc tiếp
Biết đồ thị hàm số f x = a x 4 + b x 2 + c cắt trục hoành tại 4 điểm phân biệt. Gọi S 1 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm dưới trục hoành. Gọi S 2 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm phía trên trục hoành. Cho biết 5 b 2 = 36 a c . Tính tỉ số S 1 S 2
A. S 1 S 2 = 2
B. S 1 S 2 = 1 4
C. S 1 S 2 = 1 2
D. S 1 S 2 = 1
Đáp án D
Phương trình hoành độ giao điểm của đồ thị f(x) và Ox: a x 4 + b x 2 + c = 0 .
Để phương trình có bốn nghiệm
⇔ b 2 − 4 a c > 0 − b a > 0 c a > 0 ⇔ b 2 − 5 9 b 2 > 0 − b a > 0 c a > 0 ⇔ b ≠ 0 − b a > 0 c a > 0
Gọi x 1 , x 2 , x 3 , x 4 lần lượt là bốn nghiệm của phương trình a x 4 + b x 2 + c = 0 và x 1 < x 2 < x 3 < x 4 . Không mất tính tổng quát, giả sử a>0.
Khi đó x 2 = − b + 2 b 3 2 a = − b 6 a x 2 = − b − 2 b 3 2 a = − 5 b 6 a , b < 0 .
Suy ra
x 1 = − − 5 b 6 a ; x 2 = − − b 6 a ; x 3 = − b 6 a ; x 4 = − 5 b 6 a
Do đồ thị hàm số f(x) nhận trục tung làm trục đối xứng nên ta có:
S 1 = ∫ x 1 x 2 f x d x + ∫ x 3 x 4 f x d x = − 2 ∫ x 3 x 4 f x d x = − 2 ∫ x 3 x 4 a x 4 + b x 2 + c d x
= − 2 a x 5 5 + b x 3 3 + c x x 4 x 3 = 2 a x 3 5 5 + b x 3 3 3 + c x 3 − 2 a x 4 5 5 + b x 4 3 3 + c x 4 .
S 2 = ∫ x 2 x 3 f x d x = 2 ∫ 0 x 3 f x d x = 2 ∫ 0 x 3 a x 4 + b x 2 + c d x = 2 a x 5 5 + b x 3 3 + c x x 3 0
= 2 a x 3 5 5 + 2 b x 3 3 3 + 2 c x 3 .
Suy ra
S 2 − S 1 = 2 a x 4 5 5 + 2 a x 4 3 3 + 2 c x 4 = 2 a 5 − 5 b 6 a 5 + 2 b 3 − 5 b 6 a 3 + 2 c − 5 b 6 a
= 2 a 5 . 25 b 2 36 a 2 − 5 b 6 a − 2 b 3 . 5 b 6 a − 5 b 6 a + 2 c − 5 b 6 a = − 5 b 6 a 5 b 2 18 a − 5 b 2 9 a + 2 c
= − 5 b 6 a . − 5 b 2 + 36 a c 18 a = 0
Vậy S 1 = S 2 hay S 1 S 2 = 1 .
Đúng 0
Bình luận (0)
Cho hàm số y f(x) liên tục trên R và thỏa mãn f(-1) 0 f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y f(x), y 0 và x 1. Mệnh đề nào sau đây là đúng? A. S
∫
-
1
0
f
(
x
)
d
x
+
∫
0
1
f
(
x
)...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và thỏa mãn f(-1) > 0 > f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f(x), y = 0 và x = 1. Mệnh đề nào sau đây là đúng?
A. S = ∫ - 1 0 f ( x ) d x + ∫ 0 1 f ( x ) d x
B. S = ∫ - 1 1 f ( x ) d x
C. S = ∫ - 1 1 f ( x ) d x
D. S = ∫ - 1 1 f ( x ) d x
Cho hàm số y f(x) liên tục trên đoạn [a;b] và cắt trục hoành tại điểm x c (như hình vẽ). Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị của hàm số y f(x), trục hoành và hai đường thẳng x a, x b. Khẳng định nào sau đây là khẳng định đúng?
Đọc tiếp
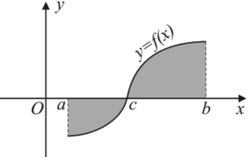
Cho hàm số y = f(x) liên tục trên đoạn [a;b] và cắt trục hoành tại điểm x = c (như hình vẽ). Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị của hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b. Khẳng định nào sau đây là khẳng định đúng?
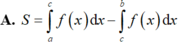
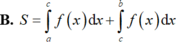
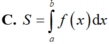
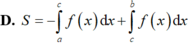
Chọn D
Ta có
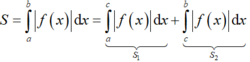
Vì f(x) < 0, ∀ x ∈ a ; c nên |f(x)| = –f(x).
Do đó, S 1 = - ∫ a c f x d x .
Tương tự, f(x) > 0, ∀ x ∈ a ; c nên |f(x)| = f(x).
Do đó, S 2 = ∫ c b f x d x .
Vậy S = - ∫ a c f x d x + ∫ c b f x d x .
Đúng 0
Bình luận (0)