Cho đường tròn tâm O bán kính R, hai dây cung AB và CD, các tia BA và DC cắt nhau tại M nằm ngoài (O) a) Biết AB=CD chứng minh MA=MC. b) Nếu AB>CD, hãy so sánh khoảng cách từ điểm M đến trung điểm của các dây AB, CD

Những câu hỏi liên quan
Cho đường tròn tâm O bán kính R, hai dây cung AB và CD, các tia BA và DC cắt nhau tại M nằm ngoài (O)
a) Biết AB=CD chứng minh MA=MC.
b) Nếu AB>CD, hãy so sánh khoảng cách từ điểm M đến trung điểm của các dây AB, CD
Cho đường tròn tâm O bán kính R, hai dây cung AB và CD, các tia BA và DC cắt nhau tại M nằm ngoài (O)
a) Biết AB=CD chứng minh MA=MC
b) Nếu AB>CD, hãy so sánh khoảng cách từ điểm M đến trung điểm của các dây AB, CD
Giúp mình với :)) Mình đang cần gấp, cảm ơn nhiều
Cho đường tròn tâm O bán kính R, hai dây cung AB và CD, các tia BA và DC cắt nhau tại M nằm ngoài (O)
a) Biết AB=CD chứng minh MA=MC.
b) Nếu AB>CD, hãy so sánh khoảng cách từ điểm M đến trung điểm của các dây AB, CD
Cho đường tròn (O;R), 2 dây cung AB và CD cắt nhau tại điểm M nằm bên trong đường tròn.
a) Cm rằng nếu AB=CD thì MA=MC
b) Trường hợp AB>CD. Hãy so sánh khoảng cách từ M đến trung điểm của các dây AB, CD (vẽ hình luôn nha)
Bài 1: Cho đường tròn (O), đường kính AB, dây CD vuông góc với AB tại điểm H thuộc bán kính OA. Gọi M là điểm thuộc bán kính OB, E và F theo thứ tự là giao điểm của CM và DM với đường tròn (E khác C, F khác D). Chứng minh rằng: a) MC MD b) ME MFBài 2: Cho đường tròn (O) đường kính AB. Vẽ các dây BC, BD thuộc hai nửa mặt phẳng đối nhau bờ AB sao cho BD BC. So sánh độ dài hai dây AD và AC.Bài 3. Cho đường tròn (O), hai dây AB và AC vuông góc với nhau có độ dài theo thứ tự bằng 10cm và 24cm. a)...
Đọc tiếp
Bài 1: Cho đường tròn (O), đường kính AB, dây CD vuông góc với AB tại điểm H thuộc bán kính OA. Gọi M là điểm thuộc bán kính OB, E và F theo thứ tự là giao điểm của CM và DM với đường tròn (E khác C, F khác D). Chứng minh rằng: a) MC = MD b) ME = MF
Bài 2: Cho đường tròn (O) đường kính AB. Vẽ các dây BC, BD thuộc hai nửa mặt phẳng đối nhau bờ AB sao cho BD > BC. So sánh độ dài hai dây AD và AC.
Bài 3. Cho đường tròn (O), hai dây AB và AC vuông góc với nhau có độ dài theo thứ tự bằng 10cm và 24cm. a) Tính khoảng cách từ tâm đến mỗi dây b) chứng minh rằng ba điểm B, O, C thẳng hàng.
Bài 4. Cho đường tròn (O), hai dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm M nằm ngoài đường tròn. Trên tia đối của tia AB lấy điểm E sao cho AE = BM. Trên tia đối của tia CD lấy điểm F sao cho CF = DM. Chứng minh rằng OE = OF.
Bài 5. Cho đường tròn (O), hai dây AB và CD có AB > CD, các tia AB và CD cắt nhau tại điểm M nằm ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. So sánh các độ dài MH và MK.
giải giúp mình vs ạ . tạo mình đang cần gấp . cảm ơn nha
Cho đường tròn tâm O bán kính R, hai dây cung AB và CD, các tia BA và DC cắt nhau tại M nằm ngoài (O)
a) Biết AB=CD chứng minh MA=MC
b) Nếu AB>CD, hãy so sánh khoảng cách từ điểm M đến trung điểm của các dây AB, CD
Câu a) Hình:
Gọi H và K lần lượt là trung điểm của AB và CD.
=> OH ⊥ AB và OK ⊥ CD ( quan hệ vuông góc giũa đường kính và dây)
Ta có: dây AB = CD (gt)
=> OH = OK ( khoảng cách từ tâm đến dây)
Xét Δ OHM và Δ OKM có:
\(\widehat{OHM}=\widehat{OKM}=90^0\)
OM: chung
OH = OK (cmt)
=> Δ OHM = Δ OKM ( cạnh huyền- cạnh góc vuông)
=> MH = MK (1)
Ta có: HB = HC = \(\frac{1}{2}AB\)
KD = KC = \(\frac{1}{2}CD\)
mà AB = CD (gt)
=> HB = KD (2)
Từ (1) và (2) cộng vế với vế ta được:
MH + HB = MK + KD
⇔ MB + MD ( đpcm)
b) Hình: tự vẽ
Gọi H và K lần lượt là trung điểm của AB và CD
=> OH ⊥ AB và OK ⊥ CD ( quan hệ vuông góc giũa đường kính và dây)
Ta có: dây AB > CD => OH < OK ( khoảng cách từ tâm đến dây)
OH < OK
⇔ OH2 < OK2 ( Chú ý: trong hình học các đoạn thẳng luôn luôn dương nghĩa là độ dài các đoạn thẳng sẽ lớn hơn hoặc bằng 0)
⇔ OH2 + OM2 < OK2 + OM2
Áp dụng dịnh lý Py - Ta - go cho các tam giác vuông OHM vuông tại H, OKM vuông tại K
ta có: MH 2 = OH2 + OM2
MK2 = OK2 + OM2
mà OH2 + OM2 < OK2 + OM2 (cmt)
=> MH2 < MK 2
⇔ MH < MK
*Chúc bạn học tốt*
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính R, hai dây cung AB và CD, các tia BA và DC cắt nhau tại M nằm ngoài (O)
a) Biết AB=CD chứng minh MA=MC
b) Nếu AB>CD, hãy so sánh khoảng cách từ điểm M đến trung điểm của các dây AB, CD
cho đường tròn tâm O, bán kính R, đường kính AB và dây cung CD cắt nhau tại M. Biết góc BMD bằng 30 độ, MC= 4 cm, MB = 12 cm. Tính khoảng cách từ O dến dây CD
Cho đường tròn tâm O, đường kính AB; dây CD cắt AB tại M. Biết MC 4 cm, MD 12 cm và
B
M
D
^
30
0
. Hãy tính:a, Khoảng cách từ O đến CDb, Bán kính của (O)
Đọc tiếp
Cho đường tròn tâm O, đường kính AB; dây CD cắt AB tại M. Biết MC = 4 cm, MD = 12 cm và B M D ^ = 30 0 . Hãy tính:
a, Khoảng cách từ O đến CD
b, Bán kính của (O)
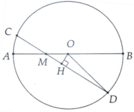
a, Gọi OH là khoảng cách từ O đến CD => MH = 4cm
Tính được OH = 4 3 3 cm
b, Tính được OD = 4 39 3 cm
Đúng 2
Bình luận (0)











