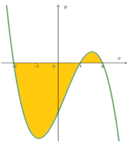
Cho đồ thị y=f(x) như hình vẽ sau đây. Biết rằng ∫ - 2 1 f ( x ) d x = a và ∫ 1 2 f ( x ) d x = b . Tính diện tích S của phần hình phẳng được tô đậm
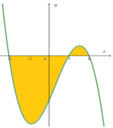
A. S=b-a
B. S=-a-b
C. S=a-b
D. S=a+b
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a;b;c;d ∈ R, a ≠ 0) có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc tọa độ và có đồ thị hàm số y = f’(x) cho bởi hình vẽ sau đây.

Tính giá trị H = f(4) – f(2)
A. H = 51
B. H = 54
C. H = 58
D. H = 64
Đáp án C
Phương pháp : Xác định hàm số f’(x) từ đó tính được ![]()
Cách giải : Ta dễ dàng tìm được phương trình parabol là
![]()
![]()
Đồ thị hàm số đi qua gốc tọa độ ![]()
![]()
Cho hàm số y=f(x). Biết rằng hàm số f(x) có đạo hàm là f’(x) và hàm số y=f’(x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây sai?
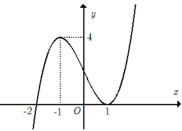
A. Hàm f(x) nghịch biến trên khoảng ( - ∞ ; - 2 )
B. Hàm f(x) đồng biến trên khoảng ( 1 ; + ∞ )
C. Trên (-1;1) thì hàm số f(x) luôn tăng.
D. Hàm f(x) giảm trên đoạn có độ dài bằng 2.
Cho hàm số y = f(x). Biết rằng hàm số f(x) có đạo hàm là f '(x) và hàm số y = f '(x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây sai?
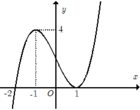
A. Hàm f (x) nghịch biến trên khoảng - ∞ ; - 2
B. Hàm f (x) đồng biến trên khoảng 1 ; + ∞
C. Trên - 1 ; 1 thì hàm số f(x) luôn tăng.
D. Hàm f(x) giảm trên đoạn có độ dài bằng 2
Biết rằng đồ thị hàm số bậc 4: y = f(x) được cho như hình vẽ sau:
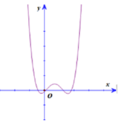
Tìm số giao điểm của đồ thị hàm số y = g(x) = [f’(x)]2 – f(x).f’’(x) và trục Ox
A. 0
B. 2
C. 4
D. 6
Đáp án A
Phương pháp:
Đặt Đáp án A
Phương pháp:
Đặt f(x) = a(x – x1)(x – x2)(x – x3)(x – x4), tính đạo hàm của hàm số y = f(x)
Xét hàm số h x = f ' x f x và chứng minh f(x).f’’(x) – [f’(x)]2 < 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Cách giải: Đồ thị hàm sốy = f(x) cắt trục hoành tại bốn điểm phân biệt nên
f(x) = a(x – x1)(x – x2)(x – x3)(x – x4)
=> f ’(x) = a(x – x1)(x – x2)(x – x3)(x – x4) + a(x – x1)(x – x3)(x – x4) + a(x – x1)(x – x2)(x – x4) + a(x – x1)(x – x2)(x – x3)
f ’(x) = f(x) 1 x - x 1 + 1 x - x 2 + 1 x - x 3 + 1 x - x 4 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4 => f’(x) ≠ 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Đặt h x = f ' x f x = 1 x - x 1 + 1 x - x 2 + 1 x - x 3 + 1 x - x 4 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Ta có
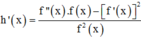
= - 1 ( x - x 1 ) 2 + - 1 ( x - x 2 ) 2 + - 1 ( x - x 3 ) 2 + - 1 ( x - x 4 ) 2 <0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
=> f ''(x).f(x) – [f’(x)]2 < 0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
=> g(x) = [f’(x)]2 – f(x).f’’(x)>0 ∀ x ∉ x 1 ; x 2 ; x 3 ; x 4
Khi f(x) = 0 => f '(x) ≠ 0 => g(x) = [f’(x)]2 – f(x).f’’(x) ≠ 0
Vậy đồ thị hàm số y = g(x) = [f’(x)]2 – f(x).f’’(x) không cắt trục Ox
Cho hàm số y=f(x) xác định, liên tục trên R và có đạo hàm f '(x). Biết rằng f '(x) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?
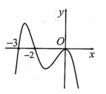
A. Hàm số y=f(x) đồng biến trên khoảng (-2;0)
B. Hàm số y=f(x) đồng biến trên khoảng ( 0 ; + ∞ )
C. Hàm số y=f(x) đồng biến trên khoảng ( - ∞ ; 3 )
D. Hàm số y=f(x) đồng biến trên khoảng (-3;-2)
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 3 + d x + e ( a ≠ 0 ) . Biết rằng hàm số f(x) có đạo hàm là f’(x) và hàm số y=f’(x) có đồ thị như hình vẽ dưới. Khi đó mệnh đề nào sau đây sai?
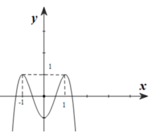
A. Hàm số f(x) nghịch biến trên khoảng (-1;1)
B. Hàm số f(x) đồng biến trên khoảng (0;+∞)
C. Hàm số f(x) đồng biến trên khoảng (-2;1)
D. Hàm số f(x) nghịch biến trên khoảng (-∞;-2)
Chọn A
Phương pháp:
Nếu f ' ( x ) ≥ 0 , ∀ x ∈ a ; b và chỉ bằng 0 tại hữu hạn điểm trên đó thì f(x) đồng biến trên khoảng (a;b).
Nếu f ' ( x ) ≤ 0 , ∀ x ∈ a ; b và chỉ bằng 0 tại hữu hạn điểm trên đó thì f(x) nghịch biến trên khoảng (a;b) Cách giải:
Quan sát đồ thị hàm số y=f’(x) , ta thấy f’(x) >0 =>Hàm số f (x) đồng biến trên
khoảng (-1;1).
=>Mệnh đề ở câu A là sai.
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Biết rằng f(x) là một trong bốn phương án A, B, C, D đưa ra dưới đây. Tìm f(x).
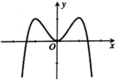
A. f(x) = x 4 - 2 x 2
B. f(x) = x 4 + 2 x 2
C. f(x) = - x 4 + 2 x 2 - 1
D. f(x) = - x 4 + 2 x 2
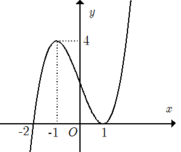
Cho hàm số y= f( x) = ax4+ bx3+ cx2+ dx+ e với a ≠0. Biết rằng hàm số y= f( x) có đạo hàm là f’(x) và hàm số y= f’(x) có đồ thị như hình vẽ bên. Khi đó nhận xét nào sau đây là sai?
A. Trên khoảng (-2; 1) thì hàm số y= f( x) luôn tăng.
B. Hàm số y= f(x) giảm trên đoạn [ -1; 1] .
C. Hàm số y= f( x) đồng biến trên khoảng (1+ ∞) .
D. Hàm số y= f( x) nghịch biến trên khoảng (- ∞; -2)
Chọn C
Trên đoạn [ - 1; 1] đồ thị hàm số y= f’( x) nằm phía trên trục hoành.
=> Trên đoạn [ - 1; 1] thì f’( x) > 0.
=> Trên đoạn [ - 1; 1] thì hàm số y= f( x) đồng biến
Cho đồ thị y=f(x) như hình vẽ sau đây. Biết rằng ∫ - 2 1 f ( x ) d x = a và ∫ 1 2 f ( x ) d x = b . Tính diện tích S của phần hình phẳng được tô đậm.
![]()
![]()
![]()
![]()