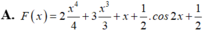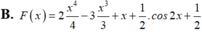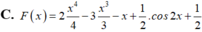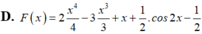Cho F(x) là một nguyên hàm của hàm số f(x). Khi đó hiệu số F(0) – F(1) bằng
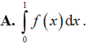
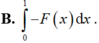

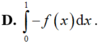
Cho F(x) là một nguyên hàm của hàm số f(x). Khi đó hiệu số F(1)-F(2) bằng
A. ∫ 1 2 f x d x
B. ∫ 1 2 - f x d x
C. ∫ 2 1 - F x d x
D. ∫ 1 2 - F x d x
Biết F(x) là một nguyên hàm của hàm số f(x) = x3 – 2x2 + 3 thỏa mãn F(1) = 3. Khi đó F(x) bằng
A. x 4 4 - 2 x 3 3 + 3 x + 5 12
B. x 4 4 - 2 x 3 3 + 3 x + 7 12
C. x 4 4 - 2 x 3 3 + 3 x + 1 12
D. 3 x 2 - 4 x + 4
Biết một nguyên hàm của hàm số f ( x ) = 1 1 - 3 x + 1 là hàm số F ( x ) thỏa mãn F ( - 1 ) = 2 3 . Khi đó F ( x ) là hàm số nào sau đây?
A. F ( x ) = x - 2 3 1 - 3 x + 3
B. F ( x ) = x - 2 3 1 - 3 x - 3
C. F ( x ) = x - 2 3 1 - 3 x + 1
D. F ( x ) = 4 - 2 3 1 - 3 x
Chọn A
F ( x ) = ∫ 1 1 - 3 x + 1 d x = - 1 3 ∫ d ( 1 - 3 x ) 1 - 3 x + x = x - 2 3 1 - 3 x + C
F ( - 1 ) = 2 3 ⇒ C = 3 ⇒ F ( x ) = x - 2 3 1 - 3 x + 3
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = sin 3 x cos x Giá trị của biểu thức F ( π 2 ) - F ( 0 ) bằng
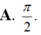
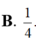
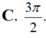
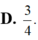
Gọi F(x) là một nguyên hàm của hàm số f(x) = xcosx thỏa mãn F(0) = 1. Khi đó phát biểu nào sau đây đúng?
A. F(x) là hàm số chẵn.
B. F(x) là hàm số lẻ.
C. Hàm số F(x) tuần hoàn với chu kì là ![]() .
.
D. Hàm số F(x) không là hàm số chẵn cũng không là hàm số lẻ.
Chọn A.
∫ x cos x d x = x sin x + cos x + C
F(0) = 1 nên C = 0. Khi đó F(x) = x.sinx + cosx
Do đó g(x) = x.sinx là hàm số chẵn; h(x)=cos x là hàm số chẵn nên F(x)= g(x) + h(x) là hàm số chẵn.
Biết F ( x ) là một nguyên hàm của hàm số f ( x ) = x 8 - x 2 thoả mãn F ( 2 ) = 0 . Khi đó phương trình F ( x ) = x có nghiệm là
A. x = 3
B. x = 1
C. x = -1
D. Tất cả sai
Chọn D
Đặt t = 8 - x 2 ⇒ t 2 = 8 - x 2 ⇒ - t d t = x d x
∫ x 8 - x 2 d x = - ∫ t d t t = - t + C = - 8 - x 2 + C
Vì F ( 2 ) = 0 nên - 8 - 4 + C = 0 suy ra C = 2.
Ta có phương trình - 8 - x 2 + 2 = x ⇔ x = 1 - 3
Biết rằng x e x là một nguyên hàm của hàm số f(-x) trên khoảng - ∞ , + ∞ . Gọi F(x) là một nguyên hàm của f ' x e x thỏa mãn F(0) =1, giá trị của F(-1) bằng:
A. 7 2
B. 5 - e 2
C. 7 - e 2
D. 5 2
Đáp án A
Phương pháp:
+) x e x là một nguyên hàm của hàm số nên x e x ' = f ( - x )
+) Từ f ( - x ) ⇒ f ( x )
+) F(x) là một nguyên hàm của f ' x e x ⇒ F ( x ) = ∫ f ' ( x ) e x d x
+) Tính F(x), từ đó tính F(-1)
Cách giải:
Vì x e x là một nguyên hàm của hàm số f ( - x ) nên x e x ' = f ( - x )
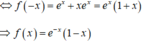
![]()
![]()
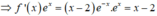
![]()
![]()
![]()
![]()
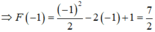
Một nguyên hàm F(x) của hàm số
f ( x ) = 2 x 3 = 3 x 2 + 1 - sin 2 x khi F(0)=1 là:
A. F x = 2 x 4 4 + 3 x 3 3 + x + 1 2 . cos 2 x + 1 2
B. F x = 2 x 4 4 - 3 x 3 3 + x + 1 2 . cos 2 x + 1 2
C. F x = 2 x 4 4 - 3 x 3 3 - x + 1 2 . cos 2 x + 1 2
D. F x = 2 x 4 4 - 3 x 3 3 + x + 1 2 . cos 2 x - 1 2
Một nguyên hàm F(x) của hàm số f ( x ) = 2 x 3 - 3 x 2 + 1 - sin 2 x khi F(0)=1 là: