Cho số phức z = x + y i x , y ∈ ℝ thỏa mãn z - 5 - 5 i = 2 2 . Tìm P = x + 2 y sao cho |z| nhỏ nhất
A. P = 12
B. P = 8
C. P = 9
D. P = 21
Cho số phức z = x + y i x , y ∈ ℝ . Tập hợp các điểm biểu diễn của số phức z sao cho số phức z + i z - i là một số thực âm là:
A. Các điểm trên trục hoành với -1 < x < 1
B. Các điểm trên trục tung với -1 < y < 1
C. Các điểm trên trục tung với - 1 ≤ y < 1
D. Các điểm trên trục tung với | y ≥ 1 y ≤ - 1
Trên mặt phẳng phức, tập hợp các số phức z = x + y i x , y ∈ ℝ thỏa mãn z + 2 + i = z ¯ - 3 i là đường thẳng có phương trình
A. y = x + 1
B. y = - x + 1
C. y = - x - 1
D. y = x - 1
Trong mặt phẳng tọa độ, tập hợp các điểm M x ; y biểu diễn của số phức z = x + y i x ; y ∈ ℝ thỏa mãn z + 1 + 3 i = z - 2 - i là
A. Đường tròn tâm O bán kính R = 1
B. Đường tròn đường kính AB với A - 1 ; - 3 và B 2 ; 1
C. Đường trung trực của đoạn thẳng AB với A - 1 ; - 3 và B 2 ; 1
D. Đường thẳng vuông góc với đoạn AB tại A với A A - 1 ; - 3 , B 2 ; 1
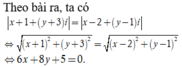
Phương trình đường trung trực của AB là: 6x + 8y + 5 = 0
Vậy tập hợp các điểm M(x;y) biểu diễn số phức z và thỏa mãn yêu cầu bài toán là đường thẳng trung trực của đoạn AB với A - 1 ; - 3 và B 2 ; 1
Chọn C.
Cho số phức z = x + iy , x , y ∈ ℝ . Tập hợp các điểm M x ; y biểu diễn số phức z là phần hình phẳng được tô màu như hình vẽ (tính cả đường viền). Khẳng định nào sau đây đúng?
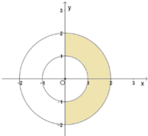
A. Số phức z có môđun nằm trong đoạn 1 ; 2 và phần thực không âm
B. Số phức z có môđun nằm trong đoạn 1 ; 2 và phần ảo không âm
C. Số phức z có môđun nằm trong khoảng 1 ; 2 và phần thực dương
D. Số phức z có môđun nằm trong đoạn 1 ; 2 và phần ảo dương
Gọi M là điểm biểu diễn số phức z = x + yi , x , y ∈ ℝ điểm biểu diễn số phức liên hợp của z bằng cách
A. Lấy đối xứng M qua trục tọa độ
B. Lấy đối xứng M qua trục hoành
C. Lấy đối xứng M qua đường thẳng y=x
D. Lấy đối xứng M qua trục tung
Đáp án B
Số phức liên hợp z ¯ = x − y i . Vậy điểm M′ biểu diễn z ¯ có được bằng cách lấy đối xứng z qua trục hoành.
Cho số phức z = a + bi(a,b ∈ ℝ ). Biết {M} biểu diễn số phức z là đường tròn x - 4 2 + y - 3 2 = 9 . Tìm max, min của F = 4a + 3b.
A. m a x F = 28 m i n F = 13
B. m a x F = 50 m i n F = 13
C. m a x F = 40 m i n F = 10
D. m a x F = 30 m i n F = 10
Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn số phức z = x + i y , x , y ∈ ℝ thỏa mãn điều kiện z = 2 .
A. Đường tròn x 2 + y 2 = 4 .
B. Đường thẳng x = 2 .
C. Đường thẳng y = 2
D. Hợp hai đường thẳng x = 2, y = 2 .
Đáp án A
z = 2 ⇔ x 2 + y 2 = 2 ⇔ x 2 + y 2 = 4 .
Gọi M là điểm biểu diễn cho số phức z =x +yi(x,y ϵ ℝ) thỏa mãn |z +1 -2i|=|z|. Tập hợp điểm là đường thẳng nào sau đây?
A. 2x +4y +5 =0.
B. 2x -4y +5 =0.
C. 2x -4y +3 =0.
D. x -2y +1= 0
Cho số phức z=3-5i. Gọi w=x+yi x , y ∈ ℝ là một căn bậc hai của z. Giá trị của biểu thức T = x 4 + y 4 là
A. T=706
B. T = 17 2
C. T = 43 2
D. T=34