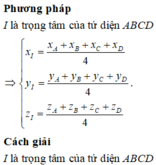
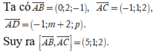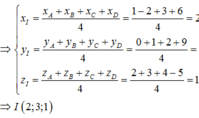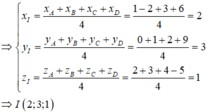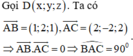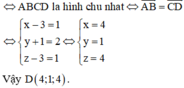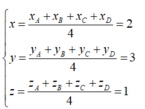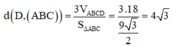Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A 1 ; 2 ; 1 , B - 2 ; 1 ; 3 , C 2 ; - 1 ; 3 . Mặt phẳng ( P ) : a x + b y + c z - 10 = 0 đi qua hai điểm A, B và cách đều hai điểm C, D và hai điểm C, D nằm khác phía so với mặt phẳng ( P ) . Tính S = a + b + c .
A. S = 7
B. S = 15
C. S = 6
D. S = 13