a/ Tam giác ABC = tam giác DMN

hay tam giác ACB = tam giác DNM

hay tam giác BAC = tam giác MDN

hay tam giác BCA = tam giác MND

hay tam giác CBA = tam giác NMD

hay tam giác CAB = tam giác NDM

b/ Ta có: tam giác ABC = tam giác DMN

=> AB = DM = 3 cm

AC = DN = 4 cm

BC = MN = 6 cm

Chu vi tam giác ABC: AB+AC+BC=3+4+6=13 cm

Chu vi tam giác DMN: DM+DN+MN=3+4+6=13 cm

Vậy chu vi tam giác ABC = 13 cm

chu vi tam giác DMN = 13 cm

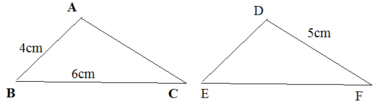
Vì ΔABC = ΔDEF nên suy ra:

    AB = DE = 4cm

    BC = EF = 6cm

    DF = AC = 5cm

Chu vi tam giác ABC bằng:

    AB + BC + CA = 4 + 6 + 5 = 15 (cm)

Chu vi tam giác DEF bằng:

    DE + EF + DF = 4 + 6 + 5 = 15 (cm)

Vì tam giác ABC = DEF

=> AB = DE = 4cm

=> AC = DF = 5cm

=> BC = EF = 6cm

=> Chu vi của 2 tam giác ABC và DEF là:

4 + 5 + 6 = 15 ( cm )

Đáp số: 15 cm

Số đo ở đâu z Trần Hải An

- Dễ mà bạn

bài 1 theo bài ra có tam giác abc=def

a=27do f=52do

mà a=d

=>a=d=27do

=> d=27 do

f=c=52do

=>c =52do

goc  b=e

ma ta co a+b+c=d+e+f=180do

thay số 27+b+52=27+e+52=180

=>b=180-(27+52)=101

=>b=e=101

Vì \(\Delta ABC=\Delta DEF\)

nên AB = DE = 4cm;

BC = EF = 6cm;

AC = DF = 5cm

Khi đó: \(P_{\Delta ABC}=P_{\Delta DEF}=4+5+6=15\left(cm\right)\)

Vậy \(P_{\Delta ABC}=P_{\Delta DEF}=15cm.\)

Ta có \(\Delta\)ABC= \(\Delta\)DEF

Suy ra: AB=DE=4cm, BC=EF=6cm, DF=AC=5cm.

Chu vi của tam giác ABC bằng: AB+BC+AC= 4+5+6=15 (cm)

Chu vi của tam giác DEF bằng: DE+EF+DF= 4+5+6=15 (cm )

vì tam giác ABC = tam giác DEF

Nên AB = DE= 4cm

BC= EF = 6 cm

AC= DF = 5 cm

lúc đó:chu vi tam giác ABC= tam giác DEF= 4+5+6=15(cm)

Vậy chu vi tam giác ABC = chu vi tam giác DEF=15cm

ta có : \(\Delta\)ABC = \(\Delta DEF\)

=>  góc A = góc D

góc B = góc E

góc C = góc F

 AB = DE = 4cm

BC  = EF = 6cm

CA = FD = 5cm

 chu vi của tam giác ABC là :

4 + 5 + 6 = 15 ( cm )

mà tam giác ABC = tam giác DEF 

=> chu vi tam giác DEF = 15 cm

a)

\(\text{Δ A'B'C' ∼ Δ ABC}\) theo tỉ số đồng dạng k = \(\dfrac{3}{5}\)

⇒ \(\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}=\dfrac{A'C'}{AC}=k=\dfrac{3}{5}\)              (1)

Áp dúng tính chất của dãy tỉ số bằng nhau, ta có:

\(\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}=\dfrac{A'C'}{AC}=\dfrac{A'B'+B'C'+A'C'}{AB+BC+AC}=\dfrac{C_{A'B'C'}}{C_{ABC}}\)                 (2)

Từ (1) và (2) ⇒ \(\dfrac{C_{A'B'C'}}{C_{ABC}}=\dfrac{3}{5}\)           (*)

b)

Theo đề ra, ta có:

\(C_{ABC}-C_{A'B'C'}=40\left(dm\right)\)

⇒ \(C_{ABC}=40+C_{A'B'C'}\)      (**)

Thay (**) vào (*), ta được:

\(\dfrac{C_{A'B'C'}}{40+C_{A'B'C'}}=\dfrac{3}{5}\)

⇒ \(5C_{A'B'C'}=120+3C_{A'B'C'}\)

⇔ \(2C_{A'B'C'}=120\)

⇒ \(C_{A'B'C'}=60\)     (dm)

⇒ \(C_{ABC}=40+60=100\)   (dm)