2x2=
2x4=
Những câu hỏi liên quan
l
i
m
x
→
+
∞
2
x
4
+
3
x
3
-
2
x
2
-
7
x
-
2
x
4...
Đọc tiếp
l i m x → + ∞ 2 x 4 + 3 x 3 - 2 x 2 - 7 x - 2 x 4 bằng:
A. 0
B. -1
C. 3/5
D. +∞
l
i
m
x
→
+
∞
2
x
4
+
x
3
-
2
x
2
-
3
x
-
2
x
4...
Đọc tiếp
l i m x → + ∞ 2 x 4 + x 3 - 2 x 2 - 3 x - 2 x 4 bằng:
A. -2
B. -1
C. 1
D. 2
so sánh mà không tính giá trị cụ thể a=2x1+2x3+2x4+...+2x99 và b=2x2+2x4+2x6+...+2x98+100
so sánh mà không tính giá trị cụ thể a=2x1+2x3+2x4+...+2x99 và b=2x2+2x4+2x6+...+2x98+100
2x4 - 10x3 - x2 + 15x - 3 ) : (2x2 - 3)
(2x4 - 10x3 - x2 +15x - 3): (2x2 - 3) = x2 - 5x + 1
Đúng 0
Bình luận (0)
Làm tính chia: (2x4 + 10x3 + x2 + 15x - 3) : (2x2 + 3)
\(=\left(2x^4+3x^2+10x^3+15x-2x^2-3\right):\left(2x^2+3\right)\\ =\left(2x^2+3\right)\left(x^2+5x-1\right):\left(2x^2+3\right)\\ =x^2+5x-1\)
Đúng 1
Bình luận (0)
Thực hiện phép chia: (2x4 – 4x3 + 5x2 + 2x – 3):(2x2 - 1)
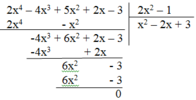
Vậy (2x4 – 4x3 + 5x2 + 2x – 3) : (2x2 – 1) = x2 – 2x + 3.
Đúng 0
Bình luận (0)
Thực hiện phép tính:
a)(x4-3x-1):(x2-x-1)
b)(x3-x2+5x-4):(-x+2x2+1)
c)(2x2+2x-5x3+2x4-1):(-x+x2+1)
\(a,=\left[x^2\left(x^2-x-1\right)+x^3+x^2-3x-1\right]:\left(x^2-x-1\right)\\ =\left[x^2\left(x^2-x-1\right)+x\left(x^2-x-1\right)+2x^2-2x-1\right]\\ =\left[x^2\left(x^2-x-1\right)+x\left(x^2-x-1\right)+2\left(x^2-x-1\right)+1\right]:\left(x^2-x-1\right)\\ =\left[\left(x^2+x+2\right)\left(x^2-x-1\right)+1\right]:\left(x^2-x-1\right)=x^2+x+2R1\)
Đúng 2
Bình luận (0)
So sánh 2 phép tính sau:
a)2x4 và 2x8;
b)2x9 và 2x2;
c)2+2x2 và 2x8+9.
a) 2 x 4 và 2 x 8
2 x 4 = 8
2 x 8 = 16
=> 2 x 4 < 2 x 8
Đúng 0
Bình luận (0)
Dễ ẹc:
a) 2 x 4 = 8
2 x 8 = 16
Mà 8 < 16
=> 2 x 4 < 2 x 8
b) 2 x 9 = 18
2 x 2 = 4
Mà 18 > 4
=> 2 x 9 > 2 x 2
c) 2 + 2 x 2 = 2 + 4 = 6
2 x 8 + 9 = 16 + 9 = 25
Mà 6 < 25
=> 2 + 2 x 2 < 2 x 8 + 9
Đúng 0
Bình luận (0)
a) Ta có : 2 x 4 = 8
2 x 8 = 16
Vì 8 < 16 \(\Rightarrow\)2 x 4 < 2 x 8
b) Ta có : 2 x 9 = 18
2 x 2 = 4
Vì 18 > 4 \(\Rightarrow\)2 x 9 > 2 x 2
c) Ta có : 2 + 2 x 2 = 2 + 4 = 6
2 x 8 + 9 = 16 + 9 = 25
Vì 6 < 25 \(\Rightarrow\)2 + 2 x 2 < 2 x 8 + 9
Đúng 0
Bình luận (0)
Xem thêm câu trả lời