Thể tích khối nón có bán kính đáy R và chiều cao h là
Đọc tiếp
Thể tích khối nón có bán kính đáy R và chiều cao h là
Những câu hỏi liên quan
Hai khối nón có cùng thể tích. Một khối nón có bán kính đáy bằng R và chiều cao bằng h, khối nón còn lại có bán kính đáy bằng 2R và chiều cao bằng x. Khi đó
Đọc tiếp
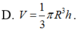
Hai khối nón có cùng thể tích. Một khối nón có bán kính đáy bằng R và chiều cao bằng h, khối nón còn lại có bán kính đáy bằng 2R và chiều cao bằng x. Khi đó
Hai khối nón có cùng thể tích. Một khối nón có bán kính đáy bằng R và chiều cao bằng h, khối nón còn lại có bán kính đáy bằng 2R và chiều cao bằng x. Khi đó A.
x
h
2
.
B.
x
h
3
2
.
C.
x
3...
Đọc tiếp
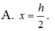
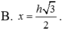
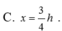
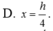
Hai khối nón có cùng thể tích. Một khối nón có bán kính đáy bằng R và chiều cao bằng h, khối nón còn lại có bán kính đáy bằng 2R và chiều cao bằng x. Khi đó
A. x = h 2 .
B. x = h 3 2 .
C. x = 3 4 h .
D. x = h 4 .
Đáp án D
Gọi V là thể tích của khối nón có bán kính đáy bằng R và chiều cao bằng h; là thể tích khối nón còn lại.
Ta có: V 1 = 1 3 π R 2 h ; V 2 = 1 3 π 2 R 2 x = 4 3 π R 2 x
Do hai khối nón có cùng thể tích nên ta có V 1 = V 2 ⇔ 1 3 π R 2 h = 4 3 π R 2 x ⇔ x = h 4 .
Đúng 0
Bình luận (0)
Cho khối cầu tâm I, bán kính R không đổi. Một khối nón có chiều cao h và bán kính đáy r, nội tiếp khối cầu. Tính chiều cao h theo bán kính R sao cho khối nón có thể tích lớn nhất.
Đọc tiếp
Cho khối cầu tâm I, bán kính R không đổi. Một khối nón có chiều cao h và bán kính đáy r, nội tiếp khối cầu. Tính chiều cao h theo bán kính R sao cho khối nón có thể tích lớn nhất.
Thể tích của khối nón có chiều cao h và bán kính đáy r là A.
V
π
r
2
h
B.
V
2
π
r
2
h
C.
V
1
6
π
r
2
h
D.
V
1
3
π
r
2...
Đọc tiếp
Thể tích của khối nón có chiều cao h và bán kính đáy r là
A. V = π r 2 h
B. V = 2 π r 2 h
C. V = 1 6 π r 2 h
D. V = 1 3 π r 2 h
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là :
Đọc tiếp
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là :
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là A.
V
πr
2
h
B.
V
1
3
r
2
h
C.
V
r
2
h
D.
V
1
3
πr
2
h
Đọc tiếp
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là
A. V = πr 2 h
B. V = 1 3 r 2 h
C. V = r 2 h
D. V = 1 3 πr 2 h
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là.
Đọc tiếp
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là.
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là : A.
V
π
r
2
h
B.
V
1
3
r
2
h
C.
V
r
2
h
D.
V
1
3
π
r
2
h
Đọc tiếp
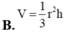
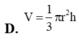
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là :
A. V = π r 2 h
B. V = 1 3 r 2 h
C. V = r 2 h
D. V = 1 3 π r 2 h
Phương pháp
Thể tích khối nón có bán kính đáy R và chiều cao h: V = 1 3 π r 2 h
Cách giải
Thể tích khối nón có bán kính đáy R và chiều cao h: V = 1 3 π r 2 h
Chọn D.
Đúng 0
Bình luận (0)
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là: A.
V
r
2
h
B.
V
1
3
π
r
2...
Đọc tiếp
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là:
A. V = r 2 h
B. V = 1 3 π r 2 h
C. V = 1 3 r 2 h
D. V = π r 2 h