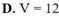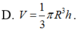Các câu hỏi tương tự
Hai khối nón có cùng thể tích. Một khối nón có bán kính đáy bằng R và chiều cao bằng h, khối nón còn lại có bán kính đáy bằng 2R và chiều cao bằng x. Khi đó
Đọc tiếp
Hai khối nón có cùng thể tích. Một khối nón có bán kính đáy bằng R và chiều cao bằng h, khối nón còn lại có bán kính đáy bằng 2R và chiều cao bằng x. Khi đó
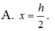
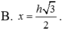
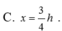
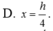
Cho khối cầu tâm I, bán kính R không đổi. Một khối nón có chiều cao h và bán kính đáy r, nội tiếp khối cầu. Tính chiều cao h theo bán kính R sao cho khối nón có thể tích lớn nhất.
Đọc tiếp
Cho khối cầu tâm I, bán kính R không đổi. Một khối nón có chiều cao h và bán kính đáy r, nội tiếp khối cầu. Tính chiều cao h theo bán kính R sao cho khối nón có thể tích lớn nhất.
![]()
![]()
![]()
![]()
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là :
Đọc tiếp
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là :
![]()
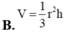
![]()
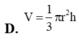
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là.
Đọc tiếp
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là.
![]()
![]()
![]()
![]()
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là: A.
V
r
2
h
B.
V
1
3
π
r
2...
Đọc tiếp
Cho khối nón có bán kính đáy là r, chiều cao h. Thể tích V của khối nón đó là:
A. V = r 2 h
B. V = 1 3 π r 2 h
C. V = 1 3 r 2 h
D. V = π r 2 h
Cho khối nón có bán kính đáy
r
2
, chiều cao
h
3
. Thể tích của khối nón là
Đọc tiếp
Cho khối nón có bán kính đáy r = 2 , chiều cao h = 3 . Thể tích của khối nón là
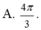
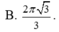
![]()
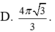
Cho khối nón có bán kính đáy r2 chiều cao, h
3
. Thể tích của khối nón là
Đọc tiếp
Cho khối nón có bán kính đáy r=2 chiều cao, h= 3 . Thể tích của khối nón là

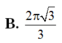
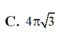
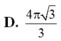
Cho khối nón có bán kính đáy
r
3
và chiều cao
h
4
. Tính thể tích V của khối nón đã cho. A.
16
π
3
3
B.
V
4
π
C.
V
16
π
3
D.
V...
Đọc tiếp
Cho khối nón có bán kính đáy r = 3 và chiều cao h = 4 . Tính thể tích V của khối nón đã cho.
A. 16 π 3 3
B. V = 4 π
C. V = 16 π 3
D. V = 12 π
Cho khối nón có bán kính đáy r = 3 và chiều cao h = 4. Tính thể tích V của khối nón đã cho
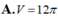
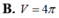
![]()