Tập hợp tất cả các điểm biểu diễn số phức z sao cho z + 3 - i z ¯ + 1 + 3 i là một số thuần ảo là một đường tròn có bán kính bằng
A. 2 2
B. 14
C. 5
D. 2
Tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn điều kiện z - i = 2 - 3 i - z là
A. Một đường tròn.
B. Một đường Elip.
C. Một đường thẳng.
D. Một đoạn thẳng.
Tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn điều kiện z - i = 2 - 3 i - z là
A. Một đường tròn
B. Một đường Elip.
C. Một đường thẳng.
D. Một đoạn thẳng.
Chọn C.
Phương pháp: Biến đổi đẳng thức đã cho.
Cách giải: Giả sử
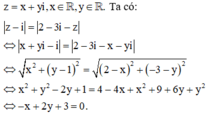
Vậy tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn điều kiện z - i = 2 - 3 i - z là một đường thẳng.
Cho số phức z thỏa mãn điều kiện |z|=3 Biết rằng tập hợp tất cả các điểm biểu diễn số phức w = 3 - 2 i + ( 2 - i ) z là một đường tròn. Bán kính của đường tròn đó là
A. R = 3 2
B. R = 3 5
C. R = 3 3
D. R = 3 7
Xét các số phức z thỏa mãn ( z ¯ +i)(z+2) là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả
các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng
A. 1
B. 5 4
C. 5 2
D. 3 2
Gọi M là điểm biểu diễn của số phức z thỏa mãn 3| z + i| = | 2 z ¯ - z + 3i | . Tập hợp tất cả những điểm M như vậy là
A. một parabol.
B. một đường thẳng.
C. một đường tròn.
D. một elip.
Chọn A.
Gọi số phức z = x + yi có điểm biểu diễn là M(x; y) trên mặt phẳng tọa độ:
Theo đề bài ta có:
![]()
⇔ |3(x + yi) + 3i| = |2(x – yi) – (x + yi) + 3i
⇔ |3x + (3y + 3)i| = |x + (3 – 3y)|
![]()
Hay 9x2 + ( 3y + 3) 2 = x2 + ( 3 - 3y) 2
Suy ra: 8x2 + 36y = 0 hay y = -2/9 x2
Vậy tập hợp các điểm M(x; y) biểu diễn số phức z theo yêu cầu của đề bài là parabol 
Cho số phức z thỏa mãn ( z + 3 - i ) ( z ¯ + 1 + 3 i ) là một số thực. Biết rằng tập hợp tất cả các điểm biểu diễn của z là một đường thẳng. Khoảng cách từ gốc tọa độ đến đường thẳng đó bằng
![]()
![]()
![]()
![]()
Tập hợp tất cả các điểm biểu diễn số phức z mà z 2 thuần ảo là
A. 1 điểm duy nhất
B. 1 đường thẳng duy nhất
C. 2 đường thẳng song song với nhau
D. 2 đường thẳng vuông góc với nhau.
Cho số phức z thay đổi thỏa mãn z - 3 - 4 i ≤ 2 . Đặt w=(z-2)(2-2i)+1, tập hợp tất cả các điểm biểu diễn số phức w là một hình tròn có diện tích bằng
A. 8 π
B. 12 π
C. 16 π
D. 32 π
Tập hợp tất cả các điểm biểu diễn số phức z = x + y i x , y ∈ R thỏa mãn z - i = 4 là đường cong có phương trình
A. x - 1 2 + y 2 = 4
B. x 2 + y - 1 2 = 4
C. x - 1 2 + y 2 = 16
D. x 2 + y - 1 2 = 16