Cho hình hộp ABCD.A'B'C'D' có thể tích V, gọi M, N là hai điểm thỏa mãn D ' M → = 2 M D → , C ' N → = 2 N C → , đường thẳng AM cắt đường thẳng A'D' tại P, đường thẳng BN cắt đường thẳng B'C' tại Q. Thể tích của khối PQNMD'C' bằng
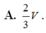
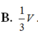
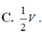
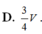
Cho hình hộp A B C D . A ' B ' C ' D ' có thể tích bằng 1. Gọi M là điểm thỏa mãn B M → = 2 3 B B ' → và N là trung điểm của DD’. Mặt phẳng (AMN) chia hình hộp thành hai phần, thể tích phần có chứa điểm A’ bằng
A. 67 144
B. 4 9
C. 3 8
D. 181 432
Chọn D.
Phương pháp:

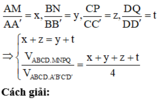
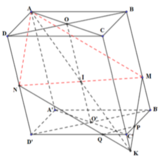
Gọi O, O’ lần lượt là tâm của các hình bình hành ABCD, A’B’C’D’.
Trong (BDD’B’), gọi I là giao điểm của OO’ và MN
Trong (ACC’A’), gọi K là giao điểm của AI và CC’
Trong (CDD’C’), gọi Q là giao điểm của NK và C’D’
Trong (CBB’C’), gọi P là giao điểm của MK và C’B’
=> Thiết diện của hình hộp cắt bởi mặt phẳng (AMN) là ngũ giác AMPQN.
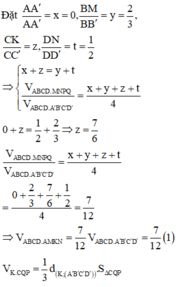
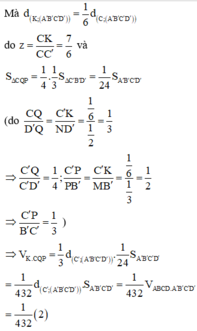
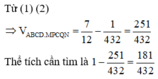
Cho hình hộp ABCD.A'B'C'D' có thể tích bằng 1. Gọi M là điểm thỏa mãn B M → = 2 3 B B ' → và N là trung điểm của DD’. Mặt phẳng (AMN) chia hình hộp thành hai phần, thể tích phần có chứa điểm A’ bằng
![]()
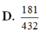
Cho hình hộp A B C D . A ' B ' C ' D ' . Gọi M là điểm thuộc đoạn CC' thỏa mãn C C ' = 3 C M . Mặt phẳng (AB'M) chia khối hộp thành hai phần có thể tích là V 1 , V 2 . Gọi V 1 là thể tích phần chứa điểm B. Tỉ số V 1 V 2 bằng
A. 7 9
B. 13 20
C. 7 27
D. 13 41
Hình hộp chữ nhật ABCD.A'B'C'D' có thể tích V. Gọi M, N lần lượt là trung điểm A’B’ và B’C’. Tính thể tích khối chóp D’.DMN.
A. V 2
B. V 4
C. V 8
D. V 16
Cho hình hộp ABCD.A'B'C'D'. Gọi E, F tương ứng là trung điểm của các cạnh A’A, C’C. Gọi M = (D'E) ∩ (DA), N = (D'F) ∩ (DC). Tính tỉ số giữa thể tích hình chóp D’.DMN và thể tích hình hộp ABCD.A'B'C'D'
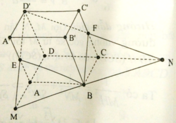
A. k = 1 3
B. k = 2 3
C. k = 3 4
D. k = 1
Đáp án B
Dễ thấy MN đi qua B, MD = 2AD, ND = 2CD. Hình chóp và hình hộp nói trên có chung chiều cao h .
Nếu diện tích đáy của hình hộp bằng S thì diện tích đáy của hình chóp bằng 2S.
Ta có:

Cho hình hộp chữ nhật ABCD.A'B'C'D' có thể tích V = a 3 . Gọi M, N, P là trung điểm BC, CD, AA'. Tính thể tích V 1 của AMNP theo a.
A. V = 1 12 a 3
B. V = 1 6 a 3
C. V = 1 8 a 3
D. V = 1 16 a 3
Cho hình hộp A B C D . A ' B ' C ' D ' . Gọi M, N, P lần lượt là trung điểm của A A ' , B C , C D . Mặt phẳng M N P chia khối hộp thành hai phần có thể tích là V 1 , V 2 . Gọi V 1 là thể tích phần chứa điểm C. Tỉ số V 1 V 2 bằng
A. 119 25
B. 3 4
C. 113 24
D. 119 425
Cho khối hộp ABCD.A'B'C'D', điểm M nằm trên cạnh CC’ thỏa mãn CC’ = 3CM. Mặt phẳng (AB’M) chia khối hộp thành hai khối đa diện. Gọi V1 là thể tích khối đa diện chứa đỉnh A’,V2 là thể tích khối đa diện chứa đỉnh B. Tính tỉ số thể tích V1 và V2.
A. 1 27
B. 27 7
C. 7 20
D. 9 4
Phương pháp:
- Dựng thiết diện cắt bởi (AB 'M) với hình hộp.
- Sử dụng phương pháp cộng trừ thể tích khối đa diện suy ra các tỉ số thể tích.
Cách giải:
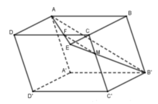
Dựng thiết diện cắt bởi (AB 'M) với hình hộp như hình vẽ.
Ta có: 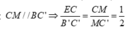
![]()
Đặt thể tích ![]()
Mà ![]()
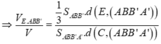
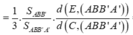
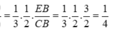
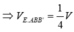
Lại có
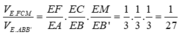
![]()
Đáp án A
Cho hình hộp ABCD.A’B’C’D’ có thể tích V, gọi M, N là hai điểm thỏa mãn D ' M → = 2 M D → , C ' N → = 2 N C → , đường thẳng AM cắt đường thẳng A’D’ tại P, đường thẳng BN cắt đường thẳng B’C’ tại Q. Thể tích của khối PQNMD’C’ bằng
A. 2 3 V
B. 1 3 V
C. 1 2 V
D. 3 4 V