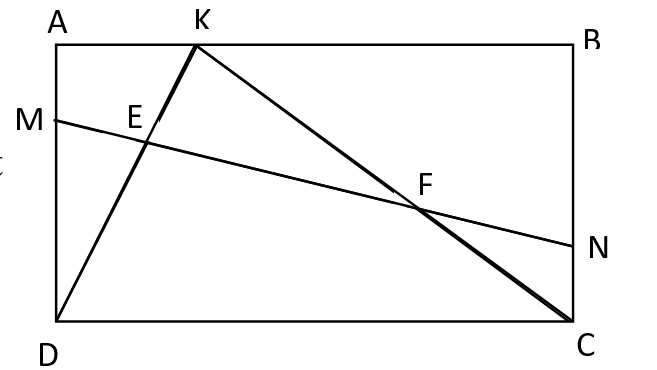
cho hình chữ nhật ABCD . Trên AD và BC lấy hai điểmM và N sao cho AM=CN..Trên AB lấy điểm K tùy ý (K không trùng với B . MN cắt KD và KC lần lượt tại E và tại F.So sánh diện tích tam giác KEF với tổng diện tích 2 hình DME và CNF

Những câu hỏi liên quan
cho hình chữ nhật ABCD . Trên AD và BC lấy hai điểmM và N sao cho AM=CN..Trên AB lấy điểm K tùy ý (K không trùng với B . MN cắt KD và KC lần lượt tại E và tại F.So sánh diện tích tam giác KEF với tổng diện tích 2 hình DME và CNF
S(KCD) = CD x BC X 1/2 = 1/2 S(ABCD)
-S(ABNM) = S(CDMN) = 1/2 s(ABCD) ( Vì AM = NC, DM = BN, AB = CD)
=> S(ABNM) = S(KCD)
=> S(CDEF) = S(AKEM) + S(BKFN) ( cùng chung S(KEF)
- Mà S(ABNM) = S(CDMN) => S(KEF) = S(DME) + S(CNF) ( cùng bớt S(CDEF) = S(AKEM) + S(BKFN))
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD . Trên CB và AD lấy điểm M và N sao cho AM = CN . Trên AB lấy K tùy ý ( khác A ; B ) MN cắt KD và KC lần lượt tại E và F . So sánh diện tích KEF và diện tích DME = diện tích CNF
Cho hình chữ nhật ABCD . Trên CB và AD lấy điểm M và N sao cho AM = CN . Trên AB lấy K tùy ý ( khác A ; B ) MN cắt KD và KC lần lượt tại E và F . So sánh diện tích KEF và diện tích DME = diện tích CNF
Cho hình chữ nhật ABCD . Trên CB và AD lấy điểm M và N sao cho AM = CN . Trên AB lấy K tùy ý ( khác A ; B ) MN cắt KD và KC lần lượt tại E và F . So sánh diện tích KEF và diện tích DME = diện tích CNF
Ai làm đúng mình cho 5 like ! ( nói thật )
cho hình chữ nhật ABCD. trên CB và AD lấy điểm M và N sao cho AM=NC. trên AB lấy K tuỳ ý ( khác A và B ). MN cắt KD và KC lần lượt tại E và F. so sánh diện tích KEF và diện tích DME + CNF
cho hình chữ nhật abcd có chu vi là 28 cm, chiều dài ab 4/3 chiều rộng ad . tính s của hình chữ nhật abcd . trên cạnh ad lấy điểm m sao cho am 1/3 ad , trên cạnh bc lấy điểm n sao cho bn md . tính diện tích hình thang mdcn ?b) trên ab lấy điểm k bất kì ( k không trùng vs a và b ).đoạn thẳng mn cắt các đoạn thẳng kd , kc lần lượt tại P và Q.so sánh diện tích tứ giác PQCD với tổng diện tích của hai hình tứ giác AMPK và BNQK? vẽ hình giúp mik với ạ
Đọc tiếp
cho hình chữ nhật abcd có chu vi là 28 cm, chiều dài ab =4/3 chiều rộng ad . tính s của hình chữ nhật abcd . trên cạnh ad lấy điểm m sao cho am = 1/3 ad , trên cạnh bc lấy điểm n sao cho bn = md . tính diện tích hình thang mdcn ?
b) trên ab lấy điểm k bất kì ( k không trùng vs a và b ).đoạn thẳng mn cắt các đoạn thẳng kd , kc lần lượt tại P và Q.so sánh diện tích tứ giác PQCD với tổng diện tích của hai hình tứ giác AMPK và BNQK?
vẽ hình giúp mik với ạ
Cho hình chữ nhật ABCD có AMNC,K bất kỳ, MN cắt KD và KC lần lượt tại E,F. So sánh diện tích tam giác KEF với tổng diện tích hai tam giác MDE và CNF.
Đọc tiếp
Cho hình chữ nhật ABCD có AM=NC,K bất kỳ, MN cắt KD và KC lần lượt tại E,F. So sánh diện tích tam giác KEF với tổng diện tích hai tam giác MDE và CNF.
Cho hình chữ nhật ABCD. Trên AD và BC ta lấy hai điểm M, N sao cho AM = CN. Lấy điểm K tùy ý trên AB, MN cắt KD và KC tại E và F. Chứng tỏ rằng: \(S_{KEF}=S_{MED}+S_{FNC}\)
Mai ơi giúp mk nhé ![]()
Sơ đồ minh họa:
Phân tích: Ta thấy tam giác \(KDC\) và tứ giác \(MNCD\) có phần chung là tứ giác \(EFCD\).
Vậy để chứng tỏ: \(S_{KEF}=S_{MED}+S_{FNC}\) ta cần chứng tỏ \(S_{KDC}=S_{MNCD}\)
Giải tóm tắt:
\(S_{KDC}=DC\times BC\div2=\frac{1}{2}\times S_{ABCD}\) (1)
Vì \(ABCD\) là hình chữ nhật nên tứ giác \(MNCD\) là hình thang và có diện tích là:
\(S_{MNCD}=\left(MD+NC\right)\times DC\div2=\)
\(=AD\times DC\div2=\frac{1}{2}\times S_{ABCD}\) (2)
Từ (1) và (2) ta có: \(S_{KDC}=S_{MNCD}\)
Tam giác \(KDC\) và hình thang \(MNCD\) có phần chung là tứ giác \(EFCD\), suy ra:
\(S_{KEF}=S_{MED}+S_{FNC}\)
Đúng 1
Bình luận (0)
Cho hình chữ nhật ABCD. Trên cạnh AB và BC là lấy 2 điểm M,N sao cho AM bằng CN. P là Một điểm bất kỳ trên cạnh AB. PD và PC lần lượt cắt MN tại I và J. So sánh diện tích tam giác PIJ với tổng diện tích hai tam giác DIM và CJN