Cho số phức z = 5-4i. Số phức đối của z có tọa độ điểm biểu diễn là
A. (-5;-4).
B. (5;4).
C. (-5;4).
D. (5;-4).
Những câu hỏi liên quan
Cho số phức z = 5 - 4 i . Số phức đối của z có tọa độ điểm biểu diễn là
A. (-5;4).
B. (5;-4).
C. (-5;-4).
D. (5;4).
Chọn A.
z = 5 - 4i ⇔ -z = -5 + 4i.
Vậy điểm biểu diễn của -z là (-5;4)
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
z
+
3
-
4
i
5
. Biết rằng tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là một đường tròn. Tim tọa độ tâm I và bán kính R của đường tròn đó. A.
I
3
;
-
4
,
R
5...
Đọc tiếp
Cho số phức z thỏa mãn z + 3 - 4 i = 5 . Biết rằng tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là một đường tròn. Tim tọa độ tâm I và bán kính R của đường tròn đó.
A. I 3 ; - 4 , R = 5
B. I - 3 ; 4 , R = 5
C. I 3 ; - 4 , R = 5
D. I - 3 ; 4 , R = 5
Cho số phức z thỏa mãn
z
+
3
−
4
i
5.
Biết rằng tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là một đường tròn. Tìm tọa độ tâm I và bán kính R của đường tròn đó. A.
I
3
;
−
4
,
R
5...
Đọc tiếp
Cho số phức z thỏa mãn z + 3 − 4 i = 5. Biết rằng tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là một đường tròn. Tìm tọa độ tâm I và bán kính R của đường tròn đó.
A. I 3 ; − 4 , R = 5 .
B. I − 3 ; 4 , R = 5 .
C. I 3 ; − 4 , R = 5.
D. I − 3 ; 4 , R = 5.
Đáp án D.
Phương pháp:
Gọi z = a + b i , sử dụng công thức tính môđun của số phức.
Cách giải:
Giả sử z = x + y i , x , y ∈ R
Theo đề bài ta có:
z + 3 − 4 i = 5 ⇔ x + 3 2 + y − 4 2 = 5 ⇔ x + 3 2 + y − 4 2 = 25
Vậy, tập hợp điểm trong mặt phẳng tọa độ biểu diễn các số phức z là đường tròn tâm I − 3 ; 4 , R = 5.
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ, số phức liên hợp của số phức
z
2
-
4
i
có điểm biểu diễn là
Đọc tiếp
Trên mặt phẳng tọa độ, số phức liên hợp của số phức z = 2 - 4 i có điểm biểu diễn là
Trên mặt phẳng tọa độ, số phức liên hợp của số phức z=2-4i có điểm biểu diễn là
A. (2;-4)
B. (-2;4)
C. (2;4)
D. (-2;-4)
Cho số phức z = 5 - 4i. Số phức liên hợp của z có điểm biểu diễn là.
A. (-5; 4)
B. (5; -4)
C. (5;4)
D. (-5; -4)
Cho số phức z=5-4i. Số phức liên hợp của z có điểm biểu diễn là
A. (-5;4)
B. (5;-4)
C. (5;4)
D. (-5;-4)
Cho số phức z có điểm biểu diễn trong mặt phẳng tọa độ Oxy là điểm
M
3
;
−
5
. Xác định số phức liên hợp
z
¯
của z. A.
z
¯
3
+
5
i
.
B.
z
¯
−
5
+
3
i
.
C...
Đọc tiếp
Cho số phức z có điểm biểu diễn trong mặt phẳng tọa độ Oxy là điểm M 3 ; − 5 . Xác định số phức liên hợp z ¯ của z.
A. z ¯ = 3 + 5 i .
B. z ¯ = − 5 + 3 i .
C. z ¯ = 5 + 3 i .
D. z ¯ = 3 − 5 i .
Điểm M biểu diễn số phức
z
5
3
-
4
i
có tọa độ là:
Đọc tiếp
Điểm M biểu diễn số phức z = 5 3 - 4 i có tọa độ là:
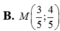
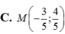
