Trong không gian Oxyz, có bao nhiêu mặt phẳng qua điểm M(4;−4;1) và chắn trên ba trục toạ độ Ox,Oy,Oz theo ba đoạn thẳng có độ dài theo thứ tự lập thành một cấp số nhân có công bội bằng 1 2 .
A. 1.
B. 2.
C. 3.
D. 4.
Trong không gian Oxyz, cho 4 điểm A(1;0;0), B(-2;0;3), M(0;0;1), N(0;3;1). Mặt phẳng (P) đi qua các điểm M, N sao cho khoảng cách từ B đến gấp hai lần khoảng cách từ A đến Có bao nhiêu mặt phẳng thỏa mãn đề bài?
A. Có hai mặt phẳng(P)
B. Chỉ có một mặt phẳng (P)
C. Không có mặt phẳng (P) nào
D. Có vô số mặt phẳng (P)
Trong không gian Oxyz cho ba điểm A(2;1;4), B(5;0;0), C(1;-3;1). Có bao nhiêu mặt cầu qua A,B,C đồng thời tiếp xúc với mặt phẳng (Oxyz)?
A. 1
B. 0
C. 2
D. Vô số
Gọi I(a,b,c) là tâm mặt cầu ta có
![]()
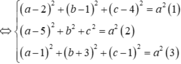
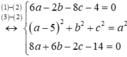
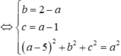
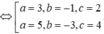
Vậy có tất cả 2 mặt cầu thoả mãn.
Chọn đáp án C.
Trong không gian Oxyz, cho điểm M(1;-3;2). có bao nhiêu mặt phẳng đi qua M và cắt các trục tọa độ tại A, B, C mà OA=OB=OC ≠ 0?
A. 3
B. 1
C. 4
D. 2
Trong không gian Oxyz, cho điểm M 1 ; − 3 ; 2 . Có bao nhiêu mặt phẳng đi qua M và cắt các trục tọa độ tại A, B, C mà O A = O B = O C ≠ 0 ?
A. 3
B. 1
C. 4
D. 2
Trong không gian Oxyz, cho điểm M(1;-3;2). Hỏi có bao nhiêu mặt phẳng đi qua M và cắt các trục tọa độ tại A, B, C mà O A = O B = O C ≠ 0 ?
A. 3.
B. 1.
C. 4.
D. 2.
Trong không gian Oxyz, có bao nhiêu đường thẳng đi qua điểm và cắt trục tọa độ Oz tại điểm N, cắt mặt phẳng tọa độ tại điểm M sao cho tam giác OMN vuông cân
A. Hai.
B. Vô số.
C. Ba.
D. Một
Trong không gian với hệ tọa độ Oxyz, cho 4 điểm A 6 ; 0 ; 0 , B 0 ; 6 ; 0 , C 2 ; 1 ; 0 và D 4 ; 3 ; − 2 . Hỏi có bao nhiêu mặt phẳng đi qua hai điểm A, B và cách đều hai điểm C, D
A. 1
B. 2
C. 3
D. 4
Đáp án B.
Kiểm tra ta được 4 điểm A, B, C, D không đồng phẳng nên tạo nên tứ diện.
- Một mặt phẳng đi qua A, B và song song với CD.
- Một mặt phẳng đi qua A, B và trung điểm CD.
Trong không gian Oxyz, cho điểm M(1;2;3). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt trục x’Ox, y’Oy, z’Oz lần lượt tại các điểm A, B, C sao cho OA = 2OB = 3OC > 0
A. 4
B. 6
C. 3
D. 2
Đáp án C
Cách giải:
Gọi tọa độ các giao điểm : A(a;0;0), B(0;b;0), C(0;0;c) (a;b;c ≠ 0)
Khi đó phương trình mặt phẳng (P) có dạng đoạn chắn: x a + y b + z c = 1
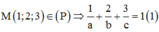
Vì OA = 2OB = 3OC > 0 nên |a| = 2|b| = 3|c| > 0

TH1: a = 2b = 3c

![]()
TH2: a = – 2b = 3c
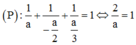
![]()
TH3: a = 2b = –3c
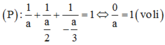
TH4: –a = 2b = –3c
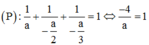
![]()
Vậy có 3 mặt phẳng (P) thỏa mãn yêu cầu đề bài
Trong không gian Oxyz, cho điểm M(1;2;3). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt trục x'Ox, y'Oy, z'Oz lần lượt tại các điểm A, B, C sao cho OA=2OB=3OC>0.
A. 4
B. 6
C. 3
D. 2
Đáp án C
Cách giải:
Gọi tọa độ các giao điểm
![]()
Khi đó phương trình mặt phẳng (P) có dạng đoạn chắn
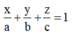
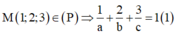
Vì OA=2OB=3OC>0 nên
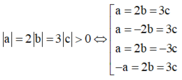
TH1: a=2b=3c
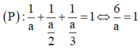
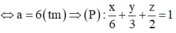
TH2: a=-2b=3c
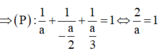
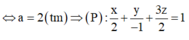
TH3: a=2b=-3c
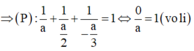
TH1: -a=2b=3c
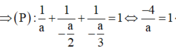
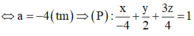
Vậy, có 3 mặt phẳng (P) thỏa mãn yêu cầu đề bài.
Trong không gian với hệ tọa độ Oxyz, cho 4 điểm A 6 ; 0 ; 0 , B 0 ; 6 ; 0 , C 2 ; 1 ; 0 và D ( 4 ; 3 ; - 2 ) . Hỏi có bao nhiêu mặt phẳng đi qua hai điểm A, B và cách đều hai điểm C, D.
A. 1
B. 2
C. 3
D. 4
Đáp án B.
Kiểm tra ta được 4 điểm A, B, C, D không đồng phẳng nên tạo nên tứ diện.
- Một mặt phẳng đi qua A, B và song song với CD.
- Một mặt phẳng đi qua A, B và trung điểm CD