Cho đồ thị hàm số y=f(x) Diện tích hình phẳng (phần có dấu gạch trong hình) là
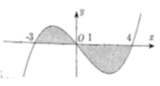
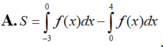
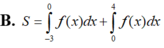
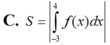
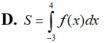
Cho đồ thị hàm số y = f(x) Diện tích hình phẳng (phần có dấu gạch trong hình) là:

A. S = ∫ - 3 0 f ( x ) d x - ∫ 0 4 f ( x ) d x
B. S = ∫ - 3 0 f ( x ) d x + ∫ 0 4 f ( x ) d x
C. S = ∫ - 3 4 f ( x ) d x
D. S = ∫ - 3 4 f ( x ) d x
Cho đồ thị hàm số y = f(x). Diện tích hình phẳng (phần có đánh dấu gạch trong hình) là:
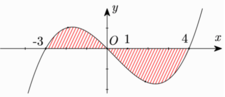
A. ∫ - 3 0 f x d x + ∫ 4 0 f x d x
B. ∫ - 3 1 f x d x + ∫ 1 4 f x d x
C. ∫ 0 - 3 f x d x + ∫ 0 4 f x d x
D. ∫ - 3 4 f x d x
Cho đồ thị hàm số y = f ( x ) . Diện tích hình phẳng (phần có đánh dấu gạch trong hình) là:
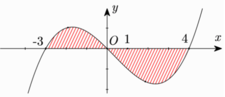
A. ∫ - 3 0 f x d x + ∫ 4 0 f x d x
B. ∫ - 3 1 f x d x + ∫ 1 4 f x d x
C. ∫ 0 - 3 f x d x + ∫ 0 4 f x d x
D. ∫ - 3 4 f x d x
Cho đồ thị hàm số y = f(x). Diện tích hình phẳng (phần gạch trong hình) là:
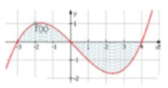
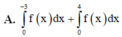
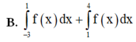
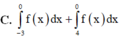
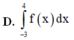
Cho đồ thị hàm số y = f(x). Diện tích hình phẳng (phần gạch trong hình) là:

A. ∫ 0 − 3 f x d x + ∫ 0 4 f x d x
B. ∫ − 3 1 f x d x + ∫ 1 4 f x d x
C. ∫ − 3 0 f x d x + ∫ 4 0 f x d x
D. ∫ − 3 4 f x d x
Đáp án C
- Vì đồ thị của hàm số f(x) cắt Ox tại điểm có hoành độ bằng 0 nên:
- Diện tích phần gạch trên hình là:
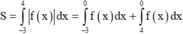
Cho đồ thị hàm số y = f(x). Diện tích hình phẳng ( phần gạch sọc ) là:
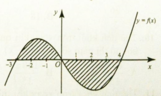
A. ∫ - 3 4 f x d x
B. ∫ - 3 1 f x d x + ∫ 1 4 f x d x
C. ∫ - 3 0 f x d x + ∫ 0 4 - f x d x
D. ∫ - 3 0 f x d x + ∫ 0 4 f x d x
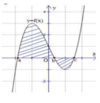
Cho hàm số y = f(x) liên tục trên Rvà có đồ thị như hình vẽ bên. Hình phẳng được đánh dấu trong hình bên có diện tích là
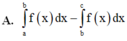
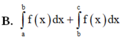
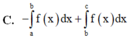
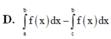
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ bên. Hình phẳng được đánh dấu trong hình bên có diện tích là
A. ∫ a b f ( x ) d x - ∫ b c f ( x ) d x
B. ∫ a b f ( x ) d x + ∫ b c f ( x ) d x
C. - ∫ a b f ( x ) d x + ∫ b c f ( x ) d x
D. ∫ a b f ( x ) d x - ∫ c b f ( x ) d x
Đáp án A
Phương pháp giải:
Áp dụng công thức tính diện tích hình phẳng giới hạn bởi y = f(x), y = 0, x = a, x = b
Lời giải:
Ta có 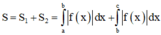
Mà 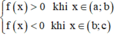
Khi đó 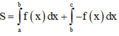
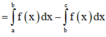
Cho hàm số y=f(x) có đồ thị hình bên thì công thức tính diện tích hình phẳng phần tô đậm trong hình là:
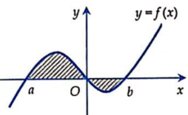
A. S = ∫ a b f x d x
B. S = ∫ a 0 f x d x + ∫ 0 b f x d x
C. S = ∫ a 0 f x d x − ∫ 0 b f x d x
D. S = ∫ a 0 f x d x − ∫ 0 b f x d x