Tìm hàm số F(x) sao cho F’(x) = f(x) nếu:

f(x) = 1/(cos⁡x)2 với x ∈ ((-π)/2; π/2). f x = 1 cos x 2 v ớ i   x ∈ - π 2 ; π 2

Cho hàm số f ( x ) = 1 + c o s x ( x - π ) 2   k h i   x ≠ π m           k h i   x = π   Tìm m để f(x) liên tục tại x = π

A.  m = 1 4

B.  m = - 1 4

C.  m = 1 2

D.  m = - 1 2

Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân  I = ∫ 0 π 3 f x d x

A.  1/2 + π/3

B.   3 + 1 2

C.   3 - 1 2

D.  1/2

Cho hàm số y = f(x) là hàm số chẵn và liên tục trên đoạn - π ; π thỏa mãn ∫ 0 π f x d x = 2018 .  Tích phân ∫ - π π f x 2018 x + 1 d x  bằng

A. 2018

B. 4036

C. 0

D.  1 2018

Cho các mệnh đề sau

(I) Hàm số f(x) = sin x x 2 + 1 là hàm số chẵn.

(II) Hàm số f(x) = 3sinx + 4cosx có giá trị lớn nhất là 5.

(III) Hàm số f(x) = tanx tuần hoàn với chu kì 2 π .

(IV) Hàm số f(x) = cosx đồng biến trên khoảng (0; π ) 

Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?

A. 4

B. 2

C. 3

D. 1

Cho hàm số y=f(x) liên tục trên  ℝ  và có đồ thị như hình bên. Phương trình f( 2 sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn  - π ; π khi và chỉ khi

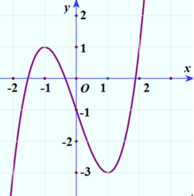
A.  m ∈ - 3 ; 1

B.  m ∈ - 3 ; 1

C.  m ∈ [ - 3 ; 1 )

D.  m ∈ ( - 3 ; 1 ]

Cho hàm số f(x)=3 sin⁡x+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số  y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng

A. 1

B. 2.

C. 4.

D. 16.

Cho hàm số f(x) thỏa mãn ∫ 0 π f ' ( x ) d x = 1 ,   f ( 0 ) = π . Tính f ( π )

A. f ( π ) = 1 - π

B.  f ( π ) = π - 1

C.  f π = π + 1

D.  f π = - π - 1

Cho F ( x ) = cos 2 x - sin x + C  là nguyên hàm của hàm số f(x). Tính  f ( π )

A.  f ( π ) = - 3

B.  f ( π ) = 1

C.  f ( π ) = - 1

D.  f ( π ) = 0