Cho tứ diện đều A B C D , A A 1 là một đường cao của tứ diện. Gọi I là trung điểm của A A 1 . Mặt phẳng (BCI) chia tứ diện đã cho thành hai tứ diện. Tính tỉ số hai bán kính của hai mặt cầu ngoại tiếp hai tứ diện đó.
A. 43 51
B. 1 2
C. 1 4
D. 48 153
Cho tứ diện đều ABCD, A A 1 là một đường cao của tứ diện. Gọi I là trung điểm của A A 1 Mặt phẳng (BCI) chia tứ diện đã cho thành hai tứ diện. Tính tỉ số hai bán kính của hai mặt cầu ngoại tiếp hai tứ diện đó
A. 43 51
B. 1 2
C. 1 4
D. 48 153
cho tứ diện SABC có đáy là tam giác đều ABC có đường cao AH=2a. Gọi O là trung điểm AH, SO vuông góc mp(ABC) và SO=2a. Gọi I là một điểm trên OH, đặt AI =x(a<x<2a). (Q) là mp qua I và (Q) vuông góc AH.
a)Xác định thiết diện của (Q) với tứ diện SABC
b) Tính diện tích thiết diện theo a và x
Cho tứ diện đều ABCD có một đường cao A A 1 . Gọi I là trung điểm A A 1 . Mặt phẳng (BCI) chia tứ diện ABCD thành hai tứ diện. Tính tỉ số hai bán kính của hai mặt cầu ngoại tiếp hai tứ diện đó.
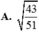
![]()
![]()
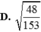
1.Cho tam giác ABC cân tại A ,AM là đường trung tuyến .GỌI D là trung điểm của AC.Lấy N đối xứng với M qua D
a)tứ giácAMCN là hình gì ?chứng minh
b)CMR: tứ giác ABMN là hình chữ nhật
c)biết AB=5 BC=6 . tính diện tích tứ giác AMCN
2.Cho hình thang cân ABCD có hay đáy AB và CD(AB<CD) .kẻ các đường cao AH và BK .CMR:
A)tứ giác ABKH là hình vuông
b) DH=CK
c)gọi E là điểm đối xứng với D qua điểm H, I là trung điểm của đoạn thẳng EB.CMR:ba điểm A,I,C thẳng hàng
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C, D và M là trung điểm của đoạn thẳng AB. Gọi T là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T).
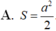
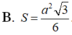
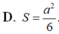
Đáp án D
Thiết diện cần tìm là MHK
Ta có:
H là trọng tâm tam giác ABE
K là trọng tâm tam giác ABF
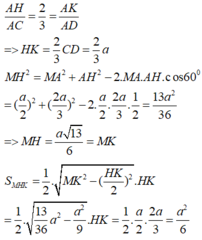
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T)
A. S = a 2 2
B. S = a 2 3 6
C. S = a 2 3 9
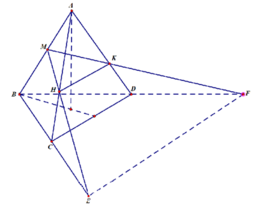
D. S = a 2 6
Đáp án D
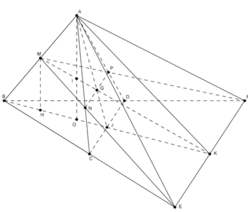

Gọi J là trung điểm CD; G là giao điểm của MK và AJ; I là giao điểm của MK và AO.
Gọi N, P lần lượt là giao điểm của ME với AC, MF với AD. Khi đó (MNP) chính là thiết diện khi cắt tứ diện đều ABCD bởi mp (MEF). Vì BE=BF=2a nên ta cũng có MN=MP, hay tam giác MNP cân tại M, đường cao MG.
Để tính diện tích MNP, ta cần đi tìm MG và NP.
Vì G là giao điểm của các đường trung tuyến AJ và MK trong tam giác ABK nên G là trọng tâm của tam giác ABK, do đó
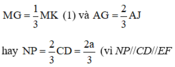
và chứng minh dựa vào các tam giác đồng dạng, tính chất tỉ số đồng dạng và các đường cao; đường cao AG, AJ trong tam giác ANP và ACD).
Áp dụng nhanh: tam giác đều cạnh a có độ dài mỗi đường cao là


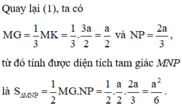
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C, D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T).
A. S = a 2 2 .
B. S = a 2 3 6 .
C. S = a 2 3 9 .
D. S = a 2 6 .
Cho tứ diện đều ABCD có cạnh bằng a. Gọi E,F lần lượt là các điểm đối xứng của B qua C,D và M là trung điểm của đoạn thẳng AB. Gọi (T) là thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MEF). Tính diện tích S của thiết diện (T)
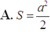


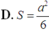
Đáp án D
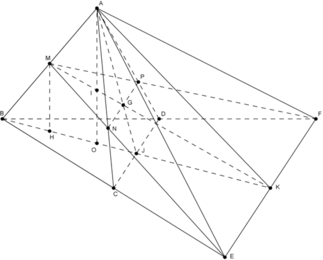
Vẽ AO ⊥ (BCD, MH ⊥ (BCD). Gọi K là trung điểm EF, ta có (ABK) ⊥ (BCD), mp (ABK) chứa AO, MH và là mặt phẳng trung trực của đoạn CD và EF.
Gọi J là trung điểm CD; G là giao điểm của MK và AJ; I là giao điểm của MK và AO.
Gọi N, P lần lượt là giao điểm của ME với AC, MF với AD. Khi đó (MNP) chính là thiết diện khi cắt tứ diện đều ABCD bởi mp (MEF). Vì BE=BF=2a nên ta cũng có MN=MP, hay tam giác MNP cân tại M, đường cao MG.
Để tính diện tích MNP, ta cần đi tìm MG và NP.
Vì G là giao điểm của các đường trung tuyến AJ và MK trong tam giác ABK nên G là trọng tâm của tam giác ABK, do đó MG = 1 3 MK (1) và AG = 2 3 AJ hay NP = 2 3 CD = 2 a 3 (vì NP//CD//EF và chứng minh dựa vào các tam giác đồng dạng, tính chất tỉ số đồng dạng và các đường cao; đường cao AG, AJ trong tam giác ANP và ACD).
Áp dụng nhanh: tam giác đều cạnh a có độ dài mỗi đường cao là 3 2 a (và diện tích là 3 4 a 2 ).
Tam giác đều BCD cạnh a có đường cao BJ = 3 2 a , trọng tâm O, suy ra BO = 2 3 BJ = a 3 . Lại vì MH là đường trung bình trong tam giác vuông ABO nên
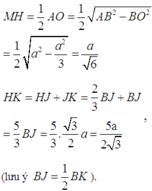
Vì tam giác MHK vuông tại H nên ta có
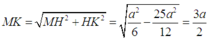
Quay lại (1), ta có
![]()
từ đó tính được diện tích tam giác MNP là
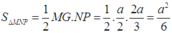
cho tam giác ABC cân tại A, đường cao AH. gọi D là trung điểm của AC. kẻ DE vuông góc AH ( E thuốc AH ) và DF vuông góc BC ( F thuộc BC )
a) cm tứ giác HEDF là hcn
b) gọi I là điểm đối xứng của A qua H. tứ giác ABIC là hình gì ? vì ?
c) tam giác ABC cần đk gì để tứ giác ABIC là hv
d) BD cắt AH tại O. tính tỉ số diện tích tam giác OBC và diện tích tứ giác HEDF