Cho hình chóp SABC có đáy là tam giác vuông tại B, AC=2a, SA vuông góc với đáy, SA=a. Tính bán kính r của mặt cầu ngoại tiếp hình chóp SABC.
A. r = a 5 2
B. r = a 2 5
C. r = 3 a 5 2
C. r = 3 a 2 5
Cho hình chóp SABC có đáy là tam giác vuông tại B, AC=2a, SA vuông góc với đáy, SA=a. Tính bán kính r của mặt cầu ngoại tiếp hình chóp SABC.
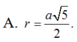
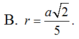
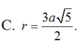
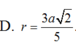
Cho hình chóp SABC có đáy là tam giác vuông tại B, AC=2a, SA vuông góc với đáy, SA=a. Bán kính r của mặt cầu ngoại tiếp hình chóp SABC bằng
![]()
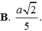
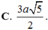
![]()
Cho hình chóp SABC có đáy là tam giác vuông tại B, A C = 2 a . SA vuông góc với đáy, S A = a . Bán kính r của mặt cầu ngoại tiếp hình chóp SABC bằng
A. a 5 2
B. a 2 5
C. 3 a 5 2
D. 3 a 2 5
cho hình chóp SABC đáy là tam giác vuông tại A, AB=a,AC=a căn 3, cạnh SA=2a. có SA vuông góc với đáy. Thể tích mặt cầu ngoại tiếp hình chóp là V. Tính V
\(BC=\sqrt{AB^2+AC^2}=2a\)
Gọi M là trung điểm BC \(\Rightarrow AM=\dfrac{1}{2}BC=a\)
GỌi N là trung điểm SA \(\Rightarrow AN=\dfrac{1}{2}SA=a\)
Dựng hình chữ nhật AMIN \(\Rightarrow\) I là tâm mặt cầu ngoại tiếp
\(R=IA=\sqrt{AM^2+AN^2}=a\sqrt{2}\)
\(\Rightarrow V=\dfrac{4}{3}\pi R^3=...\)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, cạnh bên SA vuông góc với đáy và S A = 2 a . Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC.
![]()
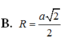
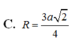
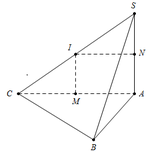
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, cạnh bên SA vuông góc với đáy và SA = 2a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC.
A. R = a 6
B. R = a 2 2
C. R = 3 a 2 4
D. R = a 6 2
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AC=6a. SA vuông góc với đáy và SA = 8a. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC
A. R = 10 a
B. R = 12 a
C. R = 5 a
D. R = 2 a
Đáp án C
Ta có: Bán kính đường tròn ngoại tiếp tam giác ABC là:
R d = A C 2 = 3 a ⇒ R = S A 2 4 + R 2 d = 5 a .
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, biết S A ⊥ ( A B C ) , S A = a , A B = 2 a , A C = 3 a . Tính bán kính r của mặt cầu ngoại tiếp hình chóp S.ABC.
A. r = 13 13 a
B. r = 3 2 a
C. r = a 14
D. r = 14 2 a
Đáp án D
Phương pháp:
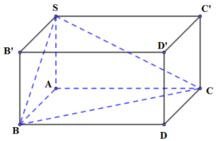
S.ABC là tứ diện vuông là một phần của hình hộp chữ nhật SB’D’C’.ABDC (như hình vẽ bên), có tâm mặt cầu ngoại tiếp trùng với tâm của hình hộp chữ nhật, có bán kính bằng nửa đường chéo của hình hộp chữ nhật (độ dài các cạnh là a, b, c) bằng 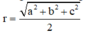
Cách giải:
Bán kính r của mặt cầu ngoại tiếp hình chóp S.ABC:
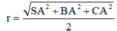
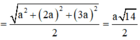
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B với A B = a , B C = a 3 . Cạnh SA vuông góc với mặt phẳng đáy và S A = 2 a 3 . Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABC
A. R = a
B. R = 3a
C. R = 4a
D. R = 2a