Nguyên hàm của hàm số f(x)=cos3x là
A. - 3 sin 3 x + C
B. - 1 3 sin 3 x + C
C. - sin 3 x + C
D. 1 3 sin 3 x + C
Tìm họ nguyên hàm của các hàm số lượng giác sau :
a) \(f\left(x\right)=\sin^3x.\sin3x\)
b) \(f\left(x\right)=\sin^3x.\cos3x+\cos^3x.\sin3x\)
a) \(f\left(x\right)=\sin^3x.\sin3x=\sin3x\left(\frac{3\sin x-\sin3x}{4}\right)=\frac{3}{4}\sin3x.\sin x-\frac{1}{4}\sin^23x\)
= \(\frac{3}{8}\left(\cos2x-\cos4x\right)-\frac{1}{8}\left(1-\cos6x\right)=\frac{3}{8}\cos2x+\frac{1}{8}\cos6x-\frac{3}{8}\cos4x-\frac{1}{8}\)
Do đó :
\(I=\int f\left(x\right)dx=\int\left(\frac{3}{8}\cos2x+\frac{1}{8}\cos6x-\frac{3}{8}\cos4x-\frac{1}{8}\right)dx=\frac{3}{16}\sin2x+\frac{1}{48}\sin6x-\frac{3}{32}\sin4x-\frac{1}{8}x+C\)
b) Ta biến đổi :
\(f\left(x\right)=\sin^3x.\cos3x+\cos^3x.\sin3x=\cos3x\left(\frac{3\sin x-\sin3x}{4}\right)+\sin3x\left(\frac{\cos3x+3\cos x}{4}\right)\)
\(=\frac{3}{4}\left(\cos3x\sin x+\sin3x\cos x\right)=\frac{3}{4}\sin4x\)
Do đó : \(I=\int f\left(x\right)dx=\frac{3}{4}\int\sin4xdx=-\frac{3}{16}\cos4x+C\)
Tìm nguyên hàm của hàm số f(x) = cos3x
![]()

![]()
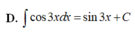
Tìm nguyên hàm của hàm số f(x) = cos3x.
A. ∫ cos 3 xdx = 3 sin 3 x + C .
B. ∫ cos 3 xdx = sin 3 x 3 + C .
C. ∫ cos 3 xdx = − sin 3 x 3 + C .
D. ∫ cos 3 xdx = sin 3 x + C .
Đáp án B
∫ cos 3 xdx = ∫ 1 3 cos 3 xd 3 x = 1 3 sin 3 x + C
Tìm nguyên hàm của hàm số f ( x ) = cos 3 x + π 6 .
A. ∫ f ( x ) d x = 1 3 sin 3 x + π 6 + C
B. ∫ f ( x ) d x = sin 3 x + π 6 + C
C. ∫ f ( x ) d x = - 1 3 sin 3 x + π 6 + C
D. ∫ f ( x ) d x = 1 6 sin 3 x + π 6 + C
Chọn A
∫
f
(
x
)
d
x
=
1
3
∫
cos
3
x
+
π
6
d
3
x
+
π
6
=
1
3
sin
3
x
+
π
6
+
C
Tìm nguyên hàm của hàm số y = f(x) = c o s 3 x .
A. ∫ f ( x ) d x = cos 4 x x + C
B. ∫ f ( x ) d x = 1 4 sin 3 x 3 + 3 sin x + C
C. ∫ f ( x ) d x = 1 12 sin 3 x - 3 4 sin x + C
D. ∫ f ( x ) d x = cos 4 x . sin x 4 + C
Tìm nguyên hàm của hàm số f(x)=3sin3x-cos3x
![]()
![]()
![]()
![]()
Tìm nguyên hàm của hàm số y = f(x) = cos 3 x

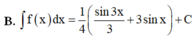
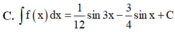

Cho các hàm số dưới đây, có bao nhiêu hàm số là hàm số chẵn:
y = cos 3 x ( 1 ) ; y = sin ( x 2 + 1 ) ( 2 ) ; y = tan 2 x ( 3 ) ; y = c o t x ( 4 )
A.1
B. 2
C. 3
D. 4
+ Xét hàm số y= f(x) = cos3x
TXĐ: D =R
Với mọi x ∈ D , ta có: - x ∈ D và
f( -x) = cos( - 3x) = cos3x = f(x)
Do đó, y= cos 3x là hàm chẵn trên tập xác định của nó.
+ Xét hàm y= g(x)= sin(x2 + 1)
TXĐ: D= R
Với mọi x ∈ D , ta có: - x ∈ D và
g( -x)= sin[ (-x)2 +1]= sin( x2+1)= g(x)
Do đó: y= sin( x2 +1) là hàm chẵn trên R.
+ Xét hàm số y= h( x)= tan2x .
TXĐ: 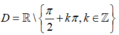
Với mọi x ∈ D , ta có: - x ∈ D và
h( -x)= tan2 (-x)= (- tanx)2 = tan2 x= h(x)
Do đó y= tan2x là hàm số chẵn trên D.
+ Xét hàm số y= t(x)= cotx.
TXĐ: ![]()
Với mọi x ∈ D , ta có: - x ∈ D và t(-x)= cot(-x) = - cotx = - t(x)
Do đó: y= cotx là hàm số lẻ trên D.
Vậy (1); (2); (3) là các hàm số chẵn
Đáp án C
Hàm số F(x) = ln|sin x – cos x| là một nguyên hàm của hàm số
A. f ( x ) = sin x + cos x sin x - cos x
B. f ( x ) = sin x - cos x sin x + cos x
C. f ( x ) = 1 sin x + cos x
D. f ( x ) = 1 sin x - cos x
Chọn A.
F ' ( x ) = sin x - cos x ' sin x - cos x = cos x + sin x sin x - cos x