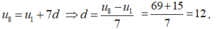Cho cấp số cộng u n với số hạng đầu là u 1 = − 2017 và công sai d = 3. Bắt đầu từ số hạng nào trở đi mà các số hạng của cấp số cộng đều nhận giá trị dương?
A. u 674
B. u 672
C. u 675
D. u 673
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
Cho cấp số cộng u n với số hạng đầu là u 1 = − 2017 và công sai d = 3. Bắt đầu từ số hạng nào trở đi mà các số hạng của cấp số cộng đều nhận giá trị dương?
A. u 674 .
B. u 672 .
C. u 675 .
D. u 673 .
Đáp án A.
Ta có: u n = u 1 + n − 1 d = − 2017 + n − 1 .3
Số hạng nhận giá trị dương khi:
− 2017 + n − 1 .3 > 0 ⇔ n − 1 > 2017 3 ⇔ n > 673 ⇒ n = 674.
Cho u n là một cấp số cộng có tổng n số hạng đầu tính được theo công thức S n = 5 n 2 + 3 n với n ∈ N * . Số hạng đầu u 1 và công sai d của cấp số cộng đó là
A. u 1 = - 8 d = 10
B. u 1 = - 8 d = - 10
C. u 1 = 8 d = 10
D. u 1 = 8 d = - 10
Cho cấp số cộng (un) có số hạng đầu là u1 = 1 và công sai d = 1. Tìm n sao cho tổng của n số hạng đầu tiên của cấp số cộng đó bằng 3003.
A. n = 79
B. n = 78
C. n = 77
D. n = 80
Chọn C
- Do công sai và số hạng đầu là d = 1, u 1 = 1 nên đây là tổng của n số tự nhiên đầu tiên là:
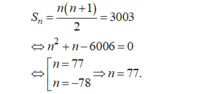
Cho cấp số cộng u n có tổng của n số hạng đầu tiên được tính bởi công thức S n = 4 n – n ^ 2. Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng. Khi đó:
A. M = -1
B. M = 1
C. M = 4
D. M = 7
Chọn B.
- Ta có: u 1 = S 1 = 3 .
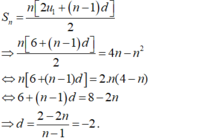
- Vậy M = u 1 + d = 3 - 2 = 1 .
Cho cấp số cộng có tổng của n số hạng đầu tiên được tính bởi công thức S n = 4 n − n 2 . Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng đó. Khi đó :
A. M=7
B. M=4
C. M= -1
D. M=1
Đáp án D
S = 1 u = 1 3 S = 2 2 u + 1 d = 4 ⇒ u = 1 3 d = − 2 ⇒ M = 1
Cho cấp số cộng có tổng của n số hạng đầu tiên được tính bởi công thức S n = 4 n − n 2 . Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng đó. Khi đó :
A. M = 7
B. M = 4
C. M = -1
D. M = 1
Đáp án D
Ta có: S = 1 u = 1 3 S = 2 2 u + 1 d = 4 ⇒ u = 1 3 d = − 2 ⇒ M = 1
Cho cấp số cộng có tổng của n số hạng đầu tiên được tính bởi công thức Sn = 4n – n2. Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng đó. Khi đó :
A. M = 7
B. M = 4
C. M = 2
D. M = 1
Một cấp số cộng gồm 8 số hạng với số hạng đầu bằng - 15 và số hạng cuối là 69. Tìm công sai của cấp số cộng.
A. -12
B. 10
C. 12
D. 10,5
Chọn C
- Theo đầu bài ta có: u 1 = - 15 ; u 8 = 69 .
- Ta có: