Tìm tất cả các giá trị thực của tham số m để hàm số y = s i n x − m x nghịch biến trên R
A. m < 1
B. m > − 1
C. m > 1
D. m ≥ 1
Tìm tất cả các giá trị thực của tham số m để hàm số y=(m-3)x-(2m+1)cosx nghịch biến trên R.
A.![]()
B. không có m
C. ![]()
D. ![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y = m - 3 x - 2 m + 1 cos x nghịch biến trên R.
A. - 4 ≤ m ≤ 2 3
B. không có m
C. 1 2 < m ≤ 3
D. - 2 ≤ m ≤ 1 2
Tìm tất cả các giá trị thực của tham số m để hàm số
y= - x 3 3 + mx 2 + 2 nghịch biến trên R
A. ![]() .
.
B.  .
.
C. 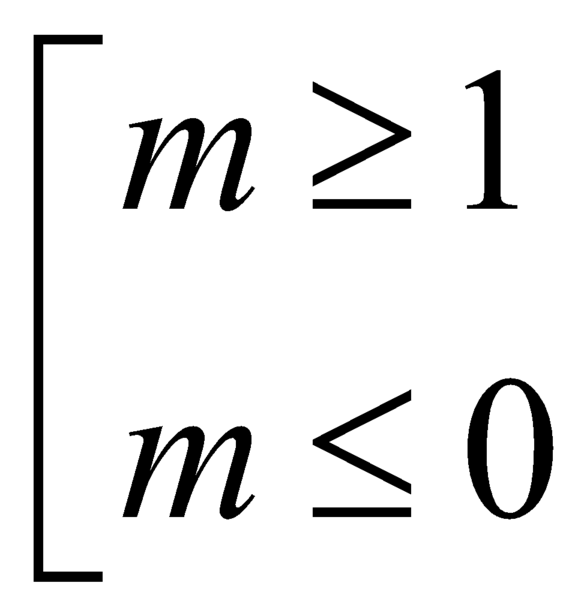 .
.
D. ![]() .
.
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y= (m-3)x- (2m+1).cos x luôn nghịch biến trên R?
A. - 4 ≤ m ≤ 2 3
B. m> 2
C. m > 3 m ≠ 1
D. m<2
Chọn A.
Tập xác định:D= R. Ta có:y ‘= m-3 + (2m+1).sinx
Hàm số nghịch biến trên R
![]()
Trường hợp 1: m= -1/ 2 ; ta có 0 ≤ 7 2 ∀ x ∈ ℝ
Vậy hàm số luôn nghịch biến trên R.
Trường hợp 2: m< -1/ 2 ; ta có
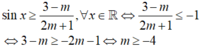
Trường hợp 3:m > -1/2 ; ta có:
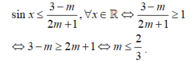
Vậy - 4 ≤ m ≤ 2 3
Tìm tất cả các giá trị thực của tham số m để hàm số y = - x 3 + 2 x 2 - ( m - 1 ) x + 2 nghịch biến trên khoảng (-∞;+∞)
A. m ≤ 7 3
B. m ≥ 7 3
C. m ≥ 1 3
D. m > 7 3
Đáp án B
Phương pháp:
Hàm số y = f(x) nghịch biến trên (-∞;+∞) khi và chỉ khi f'(x) ≤ 0, ∀ x ∈ (-∞;+∞), f'(x) = 0 tại hữu hạn điểm.
Cách giải:
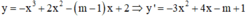
Hàm số đã cho nghịch biến trên khoảng (-∞;+∞)
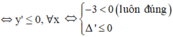
![]()
![]()
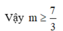
Tìm tất cả các giá trị thực của tham số m để hàm số y = m x - 4 m - x nghịch biến trên khoảng (-3;1)
A. m Î (1;2)
B. m Î [1;2)
C. m Î [1;2]
D. m Î (1;2]
Tìm tất cả các giá trị thực của tham số m để hàm số y = m x - 4 m - x nghịch biến trên khoảng (-3;1)
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y = − x 2 + (m−1)x + 2 nghịch biến trên khoảng (1; 2).
A. m < 5
B. m > 5
C. m < 3
D. m > 3
Cho hàm số y = m x + 2 2 x + m , m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số nghịch biến trên khoảng 0 ; 1 . Tìm số phần tử của S.
A. 1
B. 5
C. 2
D. 3