Cho mặt phẳng P : x + y - z + 2 = 0 ; Q : x + 1 = 0 . Gọi ∆ = P ∩ Q . Xét d : x = - 1 y = t z = 1 + t t ∈ ℝ . Chọn khẳng định đúng
![]()
![]()
![]()
![]()
trong không gian với hệ trục tọa độ oxyz, cho 2 mặt phẳng: (d) : x-z+1=0; (B) : x-4y+z-3=0. lập pt mặt phẳng (p) vuông góc với hai mặt phẳng (d),(B) và tiếp xúc với mặt cầu (S): (x-1)^2 + (y-1)^2 + (z-1)^2 = 4
Trong không gian Oxyz, cho ba mặt phẳng (P), (Q), (R) lần lượt có phương trình là ( m 2 + m)x - (m + 2)y + z = 0; x + y + z = 0; 2x + y - z = 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) đồng thời vuông góc với cả hai mặt phẳng (Q) và (R)?
A. m = 1
B. m = -1
C. m = -3/2
D. m = -3/2 hoặc m = -1
Đáp án A
Ta có:
![]()
Mặt phẳng (P) đồng thời vuông góc với cả hai mặt phẳng (Q) và (R) khi và chỉ khi
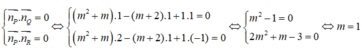
Cho ba mặt phẳng:
(P): 2x + y + z + 3 = 0
(Q): x - y - z - 1 = 0
(R): y - z + 2 = 0
Khẳng định nào sau đây là sai?
A. Không có điểm nào cùng thuộc ba mặt phẳng trên
B. (P) ⊥ (Q)
C. (P) ⊥ (R)
D. (Q) ⊥ (R)
Chọn A.
Các mặt phẳng đôi một vuông góc và có một điểm chung.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x+y+z-7=0 và đường thẳng d : x - 3 - 2 = y + 8 4 = z - 1 . Phương trình mặt phẳng (Q) chứa d đồng thời vuông góc với mặt phẳng (P) là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): x + 2 y - z - 1 = 0 , (Q): 3x-(m+2)y+(2m-1)z+3=0. Tìm m để hai mặt phẳng (P), (Q) vuông góc với nhau.
![]()
![]()
![]()
![]()
Phương trình mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng P : x+y-z-2=0, Q : x-y+z-1=0
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho đường thẳng d : x - 1 1 = y - 2 2 = z - 3 3 và mặt phẳng ( α ) : x + y - z - 2 = 0 . Trong các đường thẳng sau, đường thẳng nào nằm trong mặt phẳng ( α ) : x + y - z - 2 = 0 , đồng thời vuông góc và cắt đường thẳng d?
A. ∆ 3 : x - 5 3 = y - 2 - 2 = z - 5 1
B. ∆ 1 : x + 2 - 3 = y + 4 2 = z + 4 - 1
C. ∆ 2 : x - 2 1 = y - 4 - 2 = z - 4 3
D. ∆ 4 : x - 1 3 = y - 1 - 2 = z 1
Phương trình mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng ( P ) : x + y - z - 2 = 0 , ( Q ) : x - y + z - 1 = 0 là
A. x + y + z - 3 = 0
B. x - 2y + z = 0
C. x + z - 2 = 0
D. x + y - 2 = 0
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( P ) : x + y + z - 7 = 0 và đường thẳng d : x - 3 - 2 = y + 8 4 = z - 1 . Phương trình mặt phẳng (Q) chứa d đồng thời vuông góc với mặt phẳng (P) là:
A. (Q): 5x+y-6z+7=0
B. (Q): 5x-y-6z+7=0
C. (Q): 5x+y-6z-7=0
D. (Q): 5x-y-6z+-=0
Tìm phương trình mặt phẳng (R) đối xứng với mặt phẳng (Q) qua mặt phẳng (P) với ( P ) : x + y + z - 3 = 0 , ( Q ) : x - y - z - 4 = 0
A. 7 x + y + 2 z - 21 = 0
B. 5 x + 3 y + 3 z - 16 = 0
C. 5 x - 3 y + 3 z - 1 = 0
D. 7 x - y + 2 z + 1 = 0