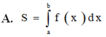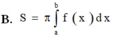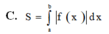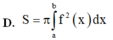Cho hình phẳng A giới hạn bởi đồ thị hai hàm số y = x 2 v à y = 6 - x .Thể tích khối tròn xoay tạo được khi quay A xung quanh trục tung là:
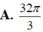
![]()
![]()
![]()
Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
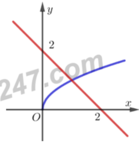
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số y = 6 và y = 6 - x và trục tùng là
A. 22 3
B. 11 3
C. 19 3
D. 25 3
Cho hình phẳng A giới hạn bởi đồ thị hai hàm số y=x2 và y=6-|x|.Thể tích khối tròn xoay tạo được khi quay A xung quanh trục tung là
A. 32π3
B. 8π
C. 9π
D. 20π
Cho hình phẳng A giới hạn bởi đồ thị hai hàm số y = x 2 và y = 6 − x . Thể tích khối tròn xoay tạo được khi quay A xung quanh trục tung là
A. 32 π 3
B. 8 π
C. 20 π
D. 6 π
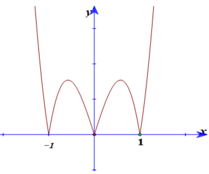
Cho hàm số y= f( x) =ax4+ bx2+ c ( a> 0) có đồ thị (C), đồ thị hàm số y= f’(x). Đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
A. 7 15
B. 8 15
C. 14 15
D. 16 15
+ Từ đồ thị của hàm số và a> 0 ta dễ dàng có được đồ thị hàm số y= f’(x) như sau:
Ta có : f’(x) = 4ax3+ 2bx
Đồ thị hàm số y= f’(x) đi qua 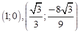 ta tìm được a=1 và b= -2
ta tìm được a=1 và b= -2
Suy ra hàm số đã cho có dạng: f(x) =x4-2x2+d và f’(x) = 4x3-4x.
+ Do (C) tiếp xúc với trục hoành nên f’(x) = 0 khi x=0; x=1; x=- 1.
Do (C) đối xứng qua trục tung nên (C) tiếp xúc với trục hoành tại 2 điểm (1; 0) và (-1; 0).
Do đó: f(0) =1 suy ra 1= 0-2.0+ d nên d= 1
Vậy hàm số cần tìm là: y =x4-2x2+1
+ Xét phương trình hoành độ giao điểm của (C) với trục hoành:
x4-2x2+1 =0 nên x=± 1
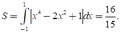
Chọn D.
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = - x 4 + 4 và y=-x+2
A. 9 2
B. 5 7
C. 8 3
D. 9
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = − x 2 + 4 v à y = - x + 2
A. 9 2
B. 5 7
C. 8 3
D. 9
Đáp án là A
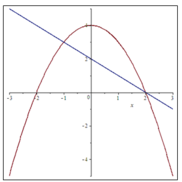
Hoành độ giao điểm của hai hàm số là

Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = - x 2 + 4 và y=-x+2
A. 9/2
B.5/7
C.8/3
D. 9
Cho hàm số y = f(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và hai đường thẳng x=a; x=b. Diện tích hình phẳng D được tính bởi công thức.