Các câu hỏi tương tự
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y
e
2
x
, trục hoành và hai đường thẳng x0 ; x3 là
Đọc tiếp
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y= e 2 x , trục hoành và hai đường thẳng x=0 ; x=3 là
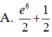
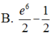


Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y
x
3
, trục hoành và hai đường thẳng x 1; x3 là A.19 B.18 C.20 D.21
Đọc tiếp
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y= x 3 , trục hoành và hai đường thẳng x= 1; x=3 là
A.19
B.18
C.20
D.21
Diện tích hình phẳng được giới hạn bởi đồ thị của hàm số
y
x
2
,
trục hoành và hai đường thẳng
x
-
1
,
x
3
l
à
:
A.
28
9
d
v
t
t...
Đọc tiếp
Diện tích hình phẳng được giới hạn bởi đồ thị của hàm số y = x 2 , trục hoành và hai đường thẳng x = - 1 , x = 3 l à :
A. 28 9 d v t t
B. 28 3 d v t t
C. 1 3 d v t t
D. Tất cả đều sai
Cho hàm số bậc ba yf(x) có đồ thị (C) như hình vẽ. Biết đồ thị hàm số đã cho cắt trục Ox tại 3 điểm có hoành độ
x
1
,
x
2
,
x
3
theo thứ tự lập thành cấp số cộng và
x
3
-
x
1
2
3
. Gọi diện tích hình phẳng giới hạn bởi (C) và trục Ox là S. Diện tích
S
1
của hình phẳng...
Đọc tiếp
Cho hàm số bậc ba y=f(x) có đồ thị (C) như hình vẽ. Biết đồ thị hàm số đã cho cắt trục Ox tại 3 điểm có hoành độ
x
1
,
x
2
,
x
3
theo thứ tự lập thành cấp số cộng và
x
3
-
x
1
=
2
3
. Gọi diện tích hình phẳng giới hạn bởi (C) và trục Ox là S. Diện tích
S
1
của hình phẳng giới hạn bởi các đường
y
=
f
x
+
1
,
y
=
-
f
x
-
1
,
x
=
x
1
và
x
=
x
3
bằng![]()
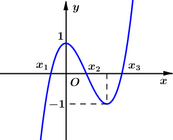
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y f(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y f(x) trục hoành và hai đường thẳng xa; xb. Diện tích hình phẳng D được tính bởi công thức.
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và hai đường thẳng x=a; x=b. Diện tích hình phẳng D được tính bởi công thức.
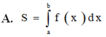
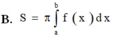
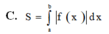
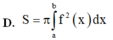
Cho hình phẳng giới hạn bởi đồ thị các hàm số
y
x
, đường thẳng y 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là A.
7
6
.
B.
4
3
.
C.
5
6
.
D.
5
4
.
Đọc tiếp
Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
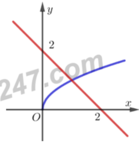
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
Cho hàm số y f( x) ax4+ bx2+ c ( a 0) có đồ thị (C), đồ thị hàm số y f’(x). Đồ thị hàm số y f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành? A.
7
15
B.
8
15
C.
14
15
D.
16
15
Đọc tiếp
Cho hàm số y= f( x) =ax4+ bx2+ c ( a> 0) có đồ thị (C), đồ thị hàm số y= f’(x). Đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
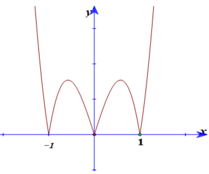
A. 7 15
B. 8 15
C. 14 15
D. 16 15
Cho hàm số y f(x) liên tục trên [a;b]. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y f(X), trục hoành và hai đường thẳng x a; x b (ab) là
Đọc tiếp
Cho hàm số y = f(x) liên tục trên [a;b]. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(X), trục hoành và hai đường thẳng x = a; x = b (a<b) là
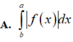
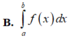
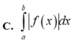
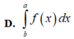
Cho hàm số
y
9
-
4
x
2
có đồ thị là (C) . Tính diện tích hình phẳng giới hạn bởi đồ thị (C ) , trục Ox, hai đường thẳng
x
3
4
và
x
3
3
4
A.
3
π
8
B.
3...
Đọc tiếp
Cho hàm số y = 9 - 4 x 2 có đồ thị là (C) . Tính diện tích hình phẳng giới hạn bởi đồ thị (C ) , trục Ox, hai đường thẳng x = 3 4 và x = 3 3 4
A. 3 π 8
B. 3 π 4
C. 3 π 16
D. 3 π 2




