Các câu hỏi tương tự
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y sin x , trục hoành và hai đường thẳng
x
π
;
x
3
π
2
là A.1 B. 1/2 C. 2 D.3/2
Đọc tiếp
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = sin x , trục hoành và hai đường thẳng x = π ; x = 3 π 2 là
A.1
B. 1/2
C. 2
D.3/2
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y
sin
2
/
3
x
, y 0 và x
π
/2 bằng:A. 1; B. 2/7;C. 2
π
; D. 2
π
/3.
Đọc tiếp
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y = sin 2 / 3 x , y = 0 và x = π /2 bằng:
A. 1; B. 2/7;
C. 2 π ; D. 2 π /3.
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
y
(
x
-
2
)
.
e
2
x
, trục tung và trục hoành. Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox có dạng
π
(
e
a
+
b...
Đọc tiếp
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = ( x - 2 ) . e 2 x , trục tung và trục hoành. Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox có dạng π ( e a + b ) c . Khi đó a+b+c bằng
A. 2
B. 56
C. -1
D. -24
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = -π/4 và x = π/4 bằng:
A. π; B. -π;
C. ln2; D. 0
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = - π /4 và x = π /4 bằng:
A. π ; B. - π ;
C. ln2; D. 0
Hình phẳng giới hạn bởi đồ thị hàm số
y
e
x
.
sin
x
và các đường thẳng x 0, x π, trục hoành. Một đường x k cắt diện tích trên tạo thành 2 phần có diện tích bằng
S
1
,
S
2
sao cho
(
2
S
1
+
2
S
2...
Đọc tiếp
Hình phẳng giới hạn bởi đồ thị hàm số y = e x . sin x và các đường thẳng x = 0, x = π, trục hoành. Một đường x = k cắt diện tích trên tạo thành 2 phần có diện tích bằng S 1 , S 2 sao cho ( 2 S 1 + 2 S 2 - 1 ) = ( 2 S 1 - 1 ) 2 khi đó k bằng:
A. π 4
B. π 2
C. π 3
D. π 6
Quay hình phẳng G giới hạn bởi các đường: y = x 3 ; y = 1, x = 0 xung quanh trục Oy. Khi đó thể tích của khối tròn xoay này bằng:
A. π B. 5 π /3
C. 3 π /5 D. 3/5
Cho hình phẳng giới hạn bởi các đường y=√x và y=x quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:
(A). 0
(B). –π
(C). π
(D). π/6
Cho hàm số bậc ba yf(x) có đồ thị (C) như hình vẽ. Biết đồ thị hàm số đã cho cắt trục Ox tại 3 điểm có hoành độ
x
1
,
x
2
,
x
3
theo thứ tự lập thành cấp số cộng và
x
3
-
x
1
2
3
. Gọi diện tích hình phẳng giới hạn bởi (C) và trục Ox là S. Diện tích
S
1
của hình phẳng...
Đọc tiếp
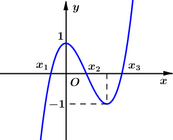
Cho hàm số bậc ba y=f(x) có đồ thị (C) như hình vẽ. Biết đồ thị hàm số đã cho cắt trục Ox tại 3 điểm có hoành độ
x
1
,
x
2
,
x
3
theo thứ tự lập thành cấp số cộng và
x
3
-
x
1
=
2
3
. Gọi diện tích hình phẳng giới hạn bởi (C) và trục Ox là S. Diện tích
S
1
của hình phẳng giới hạn bởi các đường
y
=
f
x
+
1
,
y
=
-
f
x
-
1
,
x
=
x
1
và
x
=
x
3
bằng![]()
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.