Điểm M biểu diễn số phức
z
5
3
-
4
i
có tọa độ là:
Đọc tiếp
Điểm M biểu diễn số phức z = 5 3 - 4 i có tọa độ là:
Những câu hỏi liên quan
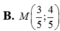
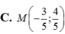
Cho M(1;2) là điểm biểu diễn số phức z. Điểm biểu diễn số phức z + 2 z ¯ có tọa độ là
A. (3;-2)
B. (2;-3)
C. (2;1)
D. (2;3)
Cho M(1;2) là điểm biểu diễn số phức z. Điểm biểu diễn số phức
z
+
2
z
có tọa độ là A. (3;-2). B. (2;-3). C. (2;1). D. (2;3).
Đọc tiếp
Cho M(1;2) là điểm biểu diễn số phức z. Điểm biểu diễn số phức z + 2 z có tọa độ là
A. (3;-2).
B. (2;-3).
C. (2;1).
D. (2;3).
Cho số phức z thỏa mãn phương trình
3
+
2
i
z
+
z
-
i
2
4
+
i
. Tìm tọa độ điểm M biểu diễn số phức z. A.
M
-
1
;
1
...
Đọc tiếp
Cho số phức z thỏa mãn phương trình 3 + 2 i z + z - i 2 = 4 + i . Tìm tọa độ điểm M biểu diễn số phức z.
A. M - 1 ; 1
B. M - 1 ; - 1
C. M 1 ; 1
D. M 1 ; - 1
Cho số phức
z
3
+
5
i
có điểm biểu diễn trên mặt phẳng tọa độ là M. Tìm tọa độ điểm M A.
M
3
;
−
5
.
B.
M
−
3
;
−
5
.
C.
M
3
;...
Đọc tiếp
Cho số phức z = 3 + 5 i có điểm biểu diễn trên mặt phẳng tọa độ là M. Tìm tọa độ điểm M
A. M 3 ; − 5 .
B. M − 3 ; − 5 .
C. M 3 ; 5 .
D. M 5 ; 3 .
Đáp án C.
Chú ý rằng số phức z = 3 + 5 i được biểu diễn bởi điểm M a ; b trên mặt phẳng tọa độ.
Đúng 0
Bình luận (0)
Biết T(4;-3) là điểm biểu diễn số phức z trên mặt phẳng tọa độ phức Oxy. Khi đó điểm nào sau đây biểu diễn số phức w = z − z ¯
A. M(1;3)
B. N(-1;-3)
C. P(-1;3)
D. Q(1;-3)
Biết T(4;-3) là điểm biểu diễn số phức z trên mặt phẳng tọa độ phức Oxy. Khi đó điểm nào sau đây biểu diễn số phức
w
z
-
z
Đọc tiếp
Biết T(4;-3) là điểm biểu diễn số phức z trên mặt phẳng tọa độ phức Oxy. Khi đó điểm nào sau đây biểu diễn số phức w = z - z
Cho số phức z có biểu diễn hình học trong mặt phẳng tọa độ Oxy là điểm M(3;-4). Môđun của z bằng
A.25
B.5
C.1
D. 5
Cho số thực a thay đổi và số phức z thỏa mãn
z
a
2
+
1
i
-
a
1
-
a
a
-
2
i
.
Trên mặt phẳng tọa độ,...
Đọc tiếp
Cho số thực a thay đổi và số phức z thỏa mãn z a 2 + 1 = i - a 1 - a a - 2 i . Trên mặt phẳng tọa độ, gọi M là điểm biểu diễn số phức z . Khoảng cách giữa hai điểm M và I (-3; 4) (khi a thay đổi) là:
A. 4
B. 3
C. 5
D. 6
Cho số phức z thỏa mãn: |z|= 4. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = (3+4i)z + i là một đường tròn có bán kính là:
A. 4.
B. 5.
C. 20.
D. 22.
Đáp án C
Đặt 
Số phức w được biểu diễn bởi điểm M (x;y).
Ta có:
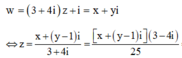
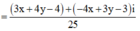
=> |z| =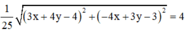 
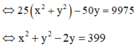
Vậy số phức w được biểu diễn bởi đường tròn tâm I (0;1), bán kính R = 20 và có phương trình: 
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn iz + 2 - i 0. Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ Oxy đến điểm M(3;-4) là: A.
2
5
B.
13
C.
2
10
D.
2
2
Đọc tiếp
Cho số phức z thỏa mãn iz + 2 - i = 0. Khoảng cách từ điểm biểu diễn của z trên mặt phẳng tọa độ Oxy đến điểm M(3;-4) là:
A. 2 5
B. 13
C. 2 10
D. 2 2
