TXĐ: .

Ta có: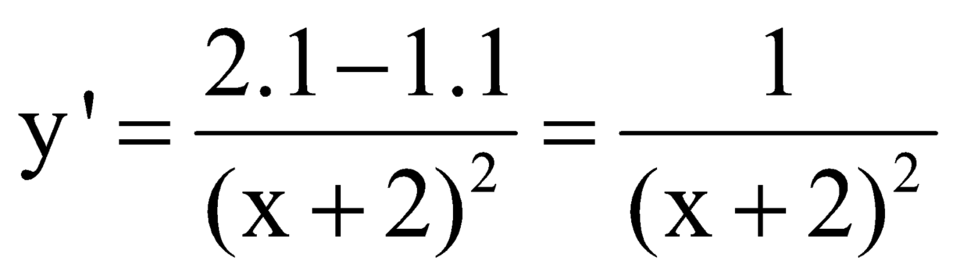

Gọi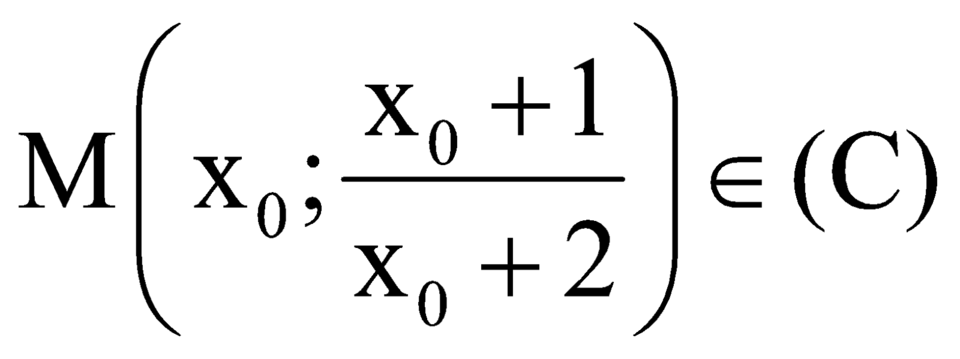 

Ta có phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ là:

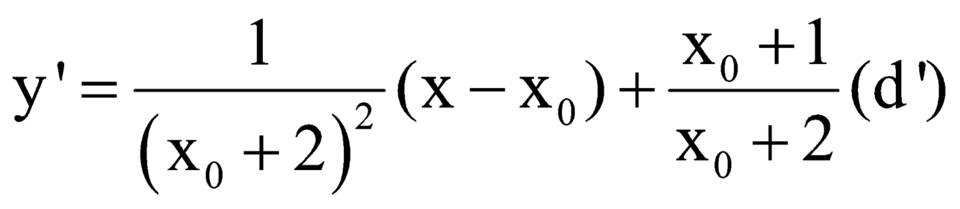
Để (vô nghiệm)

Không có điểm M nào thỏa mãn yêu cầu bài toán.

Chọn A.

Chú ý: Phải đưa phương trình đường thẳng (d) về dạng và xác định hệ số góc của đường thẳng d cho chính xác, tránh sai lầm khi cho hệ số góc của đường thẳng d trong bài toán này bằng 1

Chọn đáp án B.

Đáp án B

Đáp án A

Ta có: y ' = x − 1 − x + 3 x − 1 2 = − 4 x − 1 2 .

Tiếp tuyến tại M x 0 ; x 0 + 3 x 0 − 1 ∈ C  là:

y = − 4 x 0 − 1 2 x − x 0 + x 0 + 3 x 0 − 1 = − 4 x x 0 − 1 2 + x 0 2 + 6 x 0 − 3 x 0 − 1 2 .

Tiếp tuyến đi qua M x 1 ; 2 x 1 + 1  nên:

2 x 1 + 1 = − 4 x 1 x 0 − 1 2 + x 0 2 + 6 x 0 − 3 x 0 − 1 2    

⇔ 2 x 1 + 1 x 0 2 − 2 x 0 + 1 = x 0 2 + 6 x 0 − 3 − 4 x 1 ⇔ 2 x 1 − 1 x 0 2 − 4 x 1 + 2 x 0 + 6 x 1 + 4 = 0  (*)

Qua M x 1 ; 2 x 1 + 1  kẻ được đúng một tiếp tuyến đến đồ thị hàm số (C) nên (*) có nghiệm duy nhất

⇔ Δ ' = 4 x 1 + 2 2 − 2 x 1 − 1 6 x 1 + 4 = 0 ⇔ − 4 x 1 2 + 7 x 1 + 10 = 0 ⇔ x 1 = 7 ± 209 8 .

Vậy có 2 điểm từ đó kẻ được đúng 1 tiếp tuyến đến đồ thị hàm số.

Lần lượt thay tọa độ các điểm M, O, P, Q, A vào hàm số  f ( x )   =   3 x ta được:

+) Với M (1; 1), thay    x   =   1 ;   y   =   1 ta được 1   =   3 . 1   ⇔ 1   =   3 (vô lý) nên M  ∉   (C)

+) Với O (0; 0), thay  x   =   0 ;   y   =   0 ta được 0   =   3 . 0   ⇔ 0   =   0  (luôn đúng) nên O ∈  (C)

+) Với P (−1; −3), thay  x   =   − 1 ;   y   =   − 3 ta được − 3   =   3 . ( − 1 )   ⇔ − 3   =   − 3  (luôn đúng) nên P  ∈ (C)

+) Với Q (3; 9), thay x   =   3 ;   y   =   9   ta được 9   =   3 . 3 ⇔   9   =   9  (luôn đúng) nên Q   ∈ (C)

+) Với M (−2; 6), thay  x   =   − 2 ;   y   =   6 ta được 6   =   3 . ( − 2 )   ⇔ 6   =   − 6  (vô lý) nên A (C)

Vậy có ba điểm thuộc đồ thị (C) trong số các điểm đã cho.

Đáp án cần chọn là: B

Lần lượt thay tọa độ các điểm M, O, P, Q, A vào hàm số f ( x )   = - 1 4 x  ta được:

+) Với M (0; 4), thay x = 0; y = 4 ta được 4  = - 1 4  .0 ⇔ 4 = 0 (vô lý) nên M ∉   (C)

+) Với O (0; 0), thay  x   =   0 ;   y   =   0 ta được 0  = - 1 4 .0  ⇔ 0 = 0 (luôn đúng) nên O ∈  (C)

+) Với P (4; −1), thay  x   =   4 ;   y   =   − 1 ta được −1 = - 1 4 . 4  ⇔  1 = −1 (luôn đúng) nên P ∈  (C)

+) Với Q (−4; 1), thay  x   =   − 4 ;   y   =   1 ta được 1 = - 1 4 .(−4)  ⇔   1 = 1 (luôn đúng) nên Q  ∈  (C)

+) Với A (8; −2), thay  x   =   8 ;   y   =   − 2 ta được −2 = - 1 4 .8  ⇔ −2 = −2 (luôn đúng) nên A  ∈

Đáp án cần chọn là: A

Chọn C

Đáp án A

Gọi

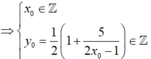
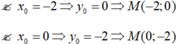
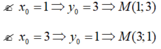
Vậy trên đồ thị (C) có bốn điểm có tọa độ là các số nguyên.

Đáp án D

Gọi .

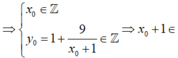
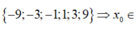
Vậy trên đồ thị (C) có sáu điểm có tọa độ là các số nguyên.