Cho hai khối trụ có cùng thể tích; bán kính đáy và chiều cao của hai khối trụ lần lượt là  R 1 ,   h 1 và R 2 ,   h 2 . Biết rằng R 1 R 2 = 3 2 . Tỉ số  h 1 h 2 bằng

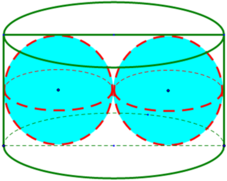
Người ta xếp hai quả cầu có cùng bán kính r vào một chiếc hộp hình trụ sao cho các quả cầu đều tiếp xúc với hai đáy, đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả cầu đều tiếp xúc với đường sinh của hình trụ ( tham khảo hình vẽ). Biết thể tích khối trụ là 120 c m 3  , thể tích của mỗi khối cầu bằng

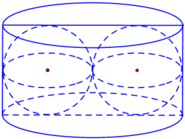
Người ta xếp hai quả cầu có cùng bán kính r vào một chiếc hộp hình trụ sao cho các quả cầu đều tiếp xúc với hai đáy, đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả cầu đề tiếp xúc với đường sinh của hình trụ ( tham khảo hình vẽ). Biết thể tích khối trụ là 120 c m 3  , thể tích của mỗi khối cầu bằng

Cho hình trụ (T) có MN , PQ vuông góc với nhau lần lượt là hai đường kinh nằm trên hai đường tròn đáy của hình trụ. Thể tích khối tứ diện MNPQ bằng 10. Tính thể tích của khối trụ (T).

A. 60 π  

B. 30 π

C. 45 π

D. 15 π

Cho hình trụ  T có MN , PQ vuông góc với nhau lần lượt là hai đường kinh nằm trên hai đường tròn đáy của hình trụ. Thể tích khối tứ diện MNPQ bằng 10. Tính thể tích của khối trụ  T .

A.  60 π

B.  30 π

C.  45 π

D.  15 π

Trong các khối trụ cùng có diện tích toàn phần là 6 π .  Tìm bán kính đáy của khối trụ có thể tích lớn nhất

A.  R   =   1

B.  R   =   1 3

C.  R   =   1 3

D.  R   =   3

Trong các khối trụ cùng có diện tích toàn phần là 6 π .  Tìm bán kính đáy của khối trụ có thể tích lớn nhất

A. R = 1

B.  R = 1 3  

C.  R = 1 3

D.  R = 3