Các câu hỏi tương tự
Cho hình trụ (T) có MN , PQ vuông góc với nhau lần lượt là hai đường kinh nằm trên hai đường tròn đáy của hình trụ. Thể tích khối tứ diện MNPQ bằng 10. Tính thể tích của khối trụ (T).
A. 60 π
B. 30 π
C. 45 π
D. 15 π
Cho hình trụ (T) có diện tích đáy bằng
48
π
và hai dây cung AB,CD lần lượt nằm trên hai đường tròn đáy của (T) sao cho ABCD là một hình vuông có độ dài cạnh bằng 10 và các cạnh của hình vuông này không song song với đường sinh của (T) (tham khảo hình vẽ bên). Tính thể tích của khối trụ (T). A. 288
π
B.
96
2
π
C.
192
2
π
D. 384...
Đọc tiếp
Cho hình trụ (T) có diện tích đáy bằng 48 π và hai dây cung AB,CD lần lượt nằm trên hai đường tròn đáy của (T) sao cho ABCD là một hình vuông có độ dài cạnh bằng 10 và các cạnh của hình vuông này không song song với đường sinh của (T) (tham khảo hình vẽ bên). Tính thể tích của khối trụ (T).
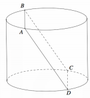
A. 288 π
B. 96 2 π
C. 192 2 π
D. 384 π
Cho hình trụ có bán kính đáy là R, độ dài đường cao là b. Đường kính MN của đáy dưới vuông góc với đường kính PQ đáy trên. Thể tích của khối tứ diện MNPQ bằng A.
2
3
R
2
h
.
B.
1
6
R
2
h
.
C.
1...
Đọc tiếp
Cho hình trụ có bán kính đáy là R, độ dài đường cao là b. Đường kính MN của đáy dưới vuông góc với đường kính PQ đáy trên. Thể tích của khối tứ diện MNPQ bằng
A. 2 3 R 2 h .
B. 1 6 R 2 h .
C. 1 3 R 2 h .
D. 2 R 2 h .
Cho hình trụ có bán kính đáy là R, độ dài đường cao là h. Đường kính MN của đáy dưới vuông góc với đường kính PQ của đáy trên. Thể tích của khối tứ diện MNPQ bằng A.
2
3
R
2
h
B.
1
6
R
2
h
C.
1
3
R
2
h
D.
2
R...
Đọc tiếp
Cho hình trụ có bán kính đáy là R, độ dài đường cao là h. Đường kính MN của đáy dưới vuông góc với đường kính PQ của đáy trên. Thể tích của khối tứ diện MNPQ bằng
A. 2 3 R 2 h
B. 1 6 R 2 h
C. 1 3 R 2 h
D. 2 R 2 h
Cho hình trụ có diện tích xung quanh bằng 4 π , thiết diện qua trục là hình vuông. Tính thể tích V của khối trụ giới hạn bởi hình trụ
A. V = 2 π
B. V = 6 π
C. V = 3 π
D. V = 5 π
Một hình trụ có bán kính r và chiều cao h r√3.a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.b) TÍnh thể tích khối trụ tạo nên bởi hình trụ đã cho.c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 300. TÍnh khoảng cách giữa đường thẳng AB và trục của hình trụ
Đọc tiếp
Một hình trụ có bán kính r và chiều cao h = r√3.
a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
b) TÍnh thể tích khối trụ tạo nên bởi hình trụ đã cho.
c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng AB và trục của hình trụ bằng 300. TÍnh khoảng cách giữa đường thẳng AB và trục của hình trụ
Một người thợ có một khối đá hình trụ. Kẻ hai đường kính MN, PQ của hai đáy sao cho
M
N
⊥
P
Q
. Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm M, N, P, Q để thu được một khối đá có hình tứ diện MNPQ. Biết rằng MN 60 cm và thể tích của khối tứ diện MNPQ bằng
30
d
m
3
. Hãy tính thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập phân) A.
111
,
4...
Đọc tiếp
Một người thợ có một khối đá hình trụ. Kẻ hai đường kính MN, PQ của hai đáy sao cho M N ⊥ P Q . Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm M, N, P, Q để thu được một khối đá có hình tứ diện MNPQ. Biết rằng MN = 60 cm và thể tích của khối tứ diện MNPQ bằng 30 d m 3 . Hãy tính thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập phân)
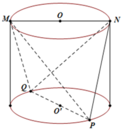
A. 111 , 4 d m 3
B. 121 , 3 d m 3
C. 101 , 3 d m 3
D. 141 , 3 d m 3
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc
45
°
. Thể tích của hình trụ bằng: A.
3
2
π
a
3
16
B. ...
Đọc tiếp
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc 45 ° . Thể tích của hình trụ bằng:
A. 3 2 π a 3 16
B. π a 3 4
C. 3 2 π a 3 8
D. 2 π a 3 16
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc
45
o
.
Tình thể tích của khối trụ. A.
3
πa
3...
Đọc tiếp
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc 45 o . Tình thể tích của khối trụ.
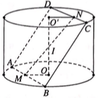
A. 3 πa 3 16 .
B . 2 πa 3 16 .
C . πa 3 16 .
D . 3 2 πa 3 16 .