Gọi tổng cần tìm là T. Tính tổng bình phương các nghiệm của phương trình: z + 1 i z + 1 i 2 . . . . z + 1 i 15 = 0
A. T = 0
B. T = 4
C. T = 15i
D. T = 15 2
Cho phương trình: x^2 + 2(m-2)x -(2m-7)=0.Gọi x1,x2 là hai nghiệm của phương trình (1).
Tìm m để phương trình (1) có tổng bình phương (1) có tổng bình phương các nghiệm đạt giá trị nhỏ nhất.
Gọi S là tổng các nghiệm phức của phương trình ( z - 1 ) 4 = 5. Tính S.
A. S = 0
B. S = 4
C. S = 2i
D. S = 4 5
Gọi T là tổng các nghiệm của phương trình l o g 2 3 x - 3 l o g 3 x + 6 = 0 , tính T
A.5
B.-3
C.36
D. 1 243
Gọi T là tổng các nghiệm của phương trình log 1 3 2 x − log 3 x + 4 = 0. Tính T.
A. T = 4
B. T = -5
C. T = 84
D. T = 5
Chọn C.
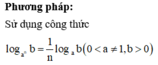
đưa phương trình về dạng phương trình bậc hai của hàm số logarit.
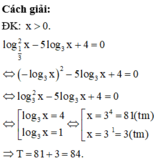
Gọi T là tổng các nghiệm của phương trình l o g 2 1 3 x - 5 l o g 3 x + 4 = 0 . Tính T
A. 4
B. -4
C. 84
D. 5
Cho phương trình
2 sin x - 1 3 tan x + 2 sin x = 3 - 4 cos 2 x . Gọi T là tập hợp các nghiệm thuộc đoạn 0 ; 20 π của phương trình trên. Tính tổng các phần tử của T
A. 570 3 π
B. 875 3 π
C. 880 3 π
D. 1150 3 π
Gọi S là tổng các giá trị thực của m để phương trình 9 z 2 + 6 z + 1 - m = 0 có nghiệm phức thỏa mãn z = 1 . Tính S
A. 20
B. 12
C. 14
D. 8
Tổng bình phương module các nghiệm của phương trình x 2 + ( i - 1 ) x + 2 + i = 0 trong tập số phức là:
A. 2
B. 6
C. 5
D. 7
Đặt T là tổng bình phương tất cả các nghiệm của phương trình
1
6
−
log
2
4
x
+
2
2
+
log
2
x
=
1.
Vậy T bằng
A. 6
B. 20
C. 36
D. 2
Đáp án B
Điều kiện:
x > 0 log 2 4 x ≠ 6 log 2 x ≠ − 2 ⇔ x > 0 x ≠ 16 x ≠ 1 4 .
1 6 − log 2 4 x + 2 2 + log 2 x = 1 ⇔ 1 4 − log 2 x + 2 2 + log 2 x = 1 ⇔ 2 + log 2 x + 8 − 2 log 2 x 4 − log 2 x 2 + log 2 x = 1 ⇔ 10 − log 2 x = − log 2 2 x + 2 log 2 x + 8 ⇔ − log 2 2 x + 3 log 2 x − 2 = 0 ⇔ log 2 x = 1 log 2 x = 2 ⇔ x = 2 x = 4 .
Vậy tổng bình phương tất cả các nghiệm của phương trình bằng 20