Tìm số nguyên n lớn nhất thỏa mãn n 360 < 3 480
A. n = 3
B. n = 4
C. n = 2
D. n = 5
Tìm các số nguyên dương n không lớn hơn 2015 thỏa mãn [n/2]+[n/3]+[n/4]=n/2+n/3+n/4 ( kí hiệu [a] là số nguyên lớn nhất không vượt quá a)
Ta có: \(\left[\frac{n}{2}\right]+\left[\frac{n}{3}\right]+\left[\frac{n}{4}\right]=\frac{n}{2}+\frac{n}{3}+\frac{n}{4}\)
Mà \(\left[\frac{n}{2}\right]+\left[\frac{n}{3}\right]+\left[\frac{n}{4}\right]\) có kết quả là số nguyên
Nên \(\frac{n}{2}+\frac{n}{3}+\frac{n}{4}\) cũng phải có kết quả là số nguyên. Hay \(\frac{n}{2};\frac{n}{3};\frac{n}{4}\) đều là số nguyên.
=> n chia hết cho cả 2;3 và 4
Vậy n sẽ là Bội của 2;3;4 hay n = 24k (k \(\in\) N*, k < 84) (BCNN(2;3;4)=24)
\(n\in\left\{24;48;72;96;120;...;1992\right\}\) Không có số 0 vì số 0 không phải là số nguyên dương.
a, Tìm các số nguyên x ,y thỏa mãn x.y=2016 và x+ y = -95
b, Tìm các số nguyên n để : 7n - 8/ 2n -3 có giá trị lớn nhất
c, Tìm các số x ,y ,z nguyên dương thỏa mãn : x^3+5x^2+21=7^y và x + 5 = 7^z
Tìm số nguyên dương n thỏa mãn:
a)A= 4n-5/n+2 là số nguyên b) B= 7n+3/n-3 là số nguyên
a) A=4n-5/n+2 = 4(n+2)-13/n+2
= 4 - 13/n+2
Để A có giá trị nguyên
=> 13/n+2 đạt giá trị nguyên
=> 13 chia hết cho (n+2)
=> n+2 thuộc Ư(13)={±1;±13}
Do n là số nguyên dương => n+2 ≥ 3 và n+2 nguyên
Hay n+2 =13
=> n=11
Vậy n=11 là giá trị nguyên dương thỏa mãn đề.
A = \(\dfrac{4n-5}{n+2}\) (đk n \(\ne\) - 2; n \(\in\) Z)
A \(\in\) Z ⇔ 4n - 5 ⋮ n + 2
4n + 8 - 13 ⋮ n + 2
4.(n + 2) - 13 ⋮ n + 2
13 ⋮ n + 2
n + 2 \(\in\) Ư(13) = {-13; -1; 1; 13}
Lập bảng ta có:
| n + 2 | -13 | -1 | 1 | 13 |
| n | -15 | -3 | -1 | 11 |
Theo bảng trên ta có: n \(\in\) {-15; -3; -1; 11}
Vì n nguyên dương nên n = 11
B = 7n+3/n-3 = 7(n-3)+24/n-3
= 7 + 24/n-3
Để B đạt giá trị nguyên
=> 24/n-3 cũng phải đạt giá trị nguyên
=> 24 chia hết cho (n-3)
=> n-3 thuộc Ư(24)={±1;±2;±3;±4;±6;±8;±12;±24}
Do n nguyên dương => n-3≥-2 và n-3 nguyên
Hay n-3 thuộc {-2;-1;1;2;3;4;6;8;12;24}
=> n thuộc {1;2;4;5;6;7;9;11;15;27}
Cho dãy số u n thỏa mãn log 3 2 u 5 - 63 = 2 log 4 u n - 8 n + 8 , ∀ n ∈ N * . Đặt S n = u 1 + u 2 + . . . + u n . Tìm số nguyên dương lớn nhất n thỏa mãn u n . S 2 n u 2 n . S n < 148 75
A. 18
B. 17
C. 16
D. 19
Tìm số nguyên n lớn nhất thỏa mãn n360 < 3480
A. n = 3
B. n = 4
C. n = 2
D. n = 5
Đáp án B
Ta có
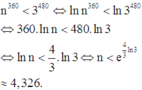
Vậy giá trị nguyên n lớn nhất thỏa mãn là n = 4
Tìm số nguyên n lớn nhất thỏa mãn n 360 < 3 480
A. n = 3
B. n = 4
C. n = 2
D. n = 5
Đáp án B
Ta có
n 360 < 3 480 ⇔ ln n 360 < ln 3 480 ⇔ 360. ln n < 480. ln 3 ⇔ ln n < 4 3 . ln 3 ⇔ n < e 4 3 ln 3 ≈ 4 , 326.
Vậy giá trị nguyên n lớn nhất thỏa mãn là n = 4.
cho biểu thức A=3/n+2 với n là số nguyên
a, số nguyên n phải thỏa mãn điều kiện gì để a là phân số
b, số nguyên n phải thỏa mãn điều kiện gì để a là số nguyên
c, tìm phân số A biết n=1, n=2, n=-7
A=3 phần n trừ 3 nhá em
Tìm số nguyên dương n lớn nhất để bất đẳng thức sau thỏa mãn
\(\frac{1}{\sqrt[n]{\left(na+b+c\right)^4}}+\frac{1}{\sqrt[n]{\left(a+nb+c\right)^4}}+\frac{1}{\sqrt[n]{\left(a+b+nc\right)^4}}\le\frac{3}{16}\)
trong đó a,b,c là các số thực dương thỏa mãn \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\le a+b+c\)
Đặt bđt là (*)
Để (*) đúng với mọi số thực dương a,b,c thỏa mãn :
\(a+b+c\ge\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)thì \(a=b=c=1\) cũng thỏa mãn (*)
\(\Rightarrow4\le\sqrt[n]{\left(n+2\right)^2}\)
Mặt khác: \(\sqrt[n]{\left(n+2\right)\left(n+2\right).1...1}\le\frac{2n+4+\left(n-2\right)}{n}=3+\frac{2}{n}\)
Hay \(n\le2\)
Với n=2 . Thay vào (*) : ta cần CM BĐT
\(\frac{1}{\left(2a+b+c\right)^2}+\frac{1}{\left(2b+c+a\right)^2}+\frac{1}{\left(2c+a+b\right)^2}\le\frac{3}{16}\)
Với mọi số thực dương a,b,c thỏa mãn: \(a+b+c\ge\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)
Vì: \(\frac{1}{\left(2a+b+c\right)^2}\le\frac{1}{4\left(a+b\right)\left(a+c\right)}\)
Tương tự ta có:
\(\frac{1}{\left(2b+a+c\right)^2}\le\frac{1}{4\left(a+b\right)\left(a+c\right)};\frac{1}{\left(2c+a+b\right)^2}\le\frac{1}{4\left(a+c\right)\left(c+b\right)}\)
Ta cần CM:
\(\frac{a+b+c}{2\left(a+b\right)\left(b+c\right)\left(c+a\right)}\le\frac{3}{16}\Leftrightarrow16\left(a+b+c\right)\le6\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
Ta có BĐT: \(9\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8\left(a+b+c\right)\left(ab+bc+ca\right)\)
Và: \(3\left(ab+cb+ac\right)\le3abc\left(a+b+c\right)\le\left(ab+cb+ca\right)^2\Rightarrow ab+bc+ca\ge3\)
=> đpcm
Dấu '=' xảy ra khi a=b=c
=> số nguyên dương lớn nhất : n=2( thỏa mãn)
các bn giúp mình giải 1 số bài tập này nhé :
-tìm số tự nhiên n thỏa mãn :n+3 chia hết cho n-2
-tìm số tự nhiên n thỏa mãn :n+3 chia hết cho 2n -2
-tìm các số nguyên x thỏa mãn x lớn hơn hoặc bằng -21/7 và x bé hơn hoặc bằng 3
-tìm các số tự nhiên x,y thỏa mãn x-1 chia hết cho y , y-1 chia hết cho x