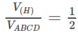Cho tứ diện có các đỉnh là A(5; 1; 3), B(1; 6; 2), C(5; 0 ; 4), D(4; 0 ; 6). Hãy viết phương trình mặt phẳng (ABC).
Ta có: AB → = (−4; 5; −1) và AC → = (0; −1; 1) suy ra n → = AB → ∧ n → = (4; 4; 4)
Do đó (ABC) có vecto pháp tuyến là n → = (4; 4; 4) hoặc n ' → = (1; 1; 1)
Suy ra phương trình của (ABC) là: (x – 5) + (y – 1) + (z – 3) = 0 hay x + y + z – 9 =0
Cho tứ diện có các đỉnh là A(5; 1; 3), B(1; 6; 2), C(5; 0; 4), D(4; 0; 6) Hãy viết phương trình của các mặt phẳng (ACD) và (BCD)
Vecto pháp tuyến của mặt phẳng (ACD) vuông góc với hai vecto A C → = 0 ; - 1 ; 1 v à A D → = - 1 ; - 1 ; 3
Cho khối tứ diện có thể tích V. Gọi V' là thể tích của khối đa diện có các đỉnh là trung điểm của các cạnh tứ diện đã cho. Tỉnh tỉ số V ' V
A. 1 4
B. 5 8
C. 3 8
D. 1 2
Cho khối tứ diện có thể tích V. Gọi V' là thể tích của khối đa diện có các đỉnh là trung điểm của các cạnh tứ diện đã cho. Tỉnh tỉ số V ' V
A. V ' V = 1 4
B. V ' V = 5 8
C. V ' V = 3 8
D. V ' V = 1 2
Chọn D.
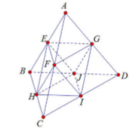
Giả sử khối tứ diện là ABCD. Gọi E, F, G, H, I, J lần lượt là trung điểm của AB. AC, AD, BC, CD, BD.
Ta có 
Do đó 
Vậy 
Cho khối tứ diện có thể tích V. Gọi V’ là thể tích khối đa diện có các đỉnh là trung điểm các cạnh của khối tứ diện đã cho. Tính tỉ số V ' V
A . V ' V = 2 3
B . V ' V = 1 4
C . V ' V = 5 8
D . V ' V = 1 2
Cho tứ diện có thể tích bằng V. Gọi V’ là thể tích của khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho, tính tỉ số V ' V
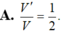
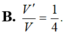
Đáp án A
Gọi M,N,P,Q,H,R lần lượt là trung điểm của SA,SC,BC,AB,AC,SB
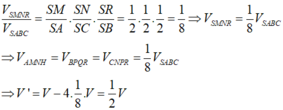
Cho tứ diện có thể tích bằng V. Gọi V’ là thể tích của khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho, tính tỉ số V ' V .
A. V ' V = 1 2 .
B. V ' V = 1 4 .
C. V ' V = 2 3 .
D. V ' V = 5 8 .
Đáp án A
Gọi M,N,P,Q,H,R lần lượt là trung điểm của SA,SC,BC,AB,AC,SB
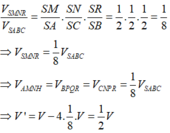
Cho tứ diện OABC có các góc tại đỉnh O đều bằng 90 ° và O A = a , O B = b ; O C = c . Gọi G là trọng tâm của tứ diện. Thể tích của khối tứ diện GABC bằng
A. a b c 6
B. a b c 8
C. a b c 4
D. a b c 24
Chọn D.
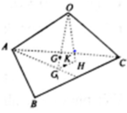
Gọi G1 là trọng tâm của tam giác ABC, H và K lần lượt là hình chiếu của O và G trên mặt phẳng (ABC). Khi đó
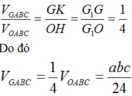
Cho một khối tứ diện có thể tích V. Gọi V ' là thể tích khối đa diện có các đỉnh là trung điểm các cạnh của khối tứ diện đã cho. Tính tỉ số V V '
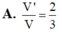
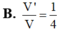
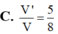
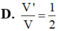
Cho tứ diện đều ABCD. Gọi (H) là hình bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện đều đó. Tính tỉ số: V H V ABCD
Gọi cạnh của tứ diện đều ABCD là a thì cạnh của hình bát diện đều (H) là a/2. Khi đó
Từ đó suy ra 
