Cho số thực a > 2 và gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 - 2 z + a . Mệnh đề nào sau đây sai?
A. z 1 + z 2 là số thực
B. z 1 - z 2 là số ảo
C. z 1 z 2 + z 2 z 1 là số ảo
D. z 1 z 2 + z 2 z 1 là số thực
Gọi z1; z2 là hai nghiệm phức của phương trình z2 – z + 1 = 0 . Tìm phần thực, phần ảo của số phức ![]() lần lượt là?
lần lượt là?
A. 0; 1
B. 1; 0
C. -1; 0
D. 0; -1
Chọn C.
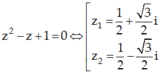
Ta có 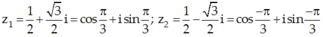
Áp dụng công thức Moa-vrơ:
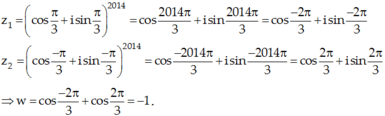
Phần thực của w là -1, phần ảo là 0.
Cho số phức z và gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 + 8 i = 0 (có z 1 có phần thực dương). Giá trị nhỏ nhất của biểu thức P = z - z 1 + z 2 - z + z ¯ + 2 z 1 + z 2 2 được viết dưới dạng m n + p q (trong đó n , p ∈ N ; m , q là các số nguyên tố). Tổng m + n + p + q bằng
A. 10
B. 13
C. 11
D. 12
Cho z = a + bi là một số phức. Hãy tìm phương trình bậc hai với hệ số thực nhận z và z làm nghiệm.
Cho số phức z = - 1 2 + i 3 2 . Phương trình bậc hai với hệ số thực nhận z và z làm nghiệm là
A. z 2 - z + 2 = 0
B. 2 z 2 + z + 2 = 0
C. z 2 - z + 1 = 0
D. z 2 + z + 1 = 0
Trong tập các số phức gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 với z 2 có phần ảo dương. Cho số phức z thỏa mãn |z- z 1 | = 1 Giá trị nhỏ nhất của P = |z- z 2 | là
A . 2016 - 1
B . 2017 - 1
C . 2017 - 1 2
D . 2016 - 1 2
Đáp án A
Phương trình 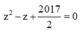
![]()
![]()
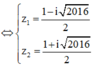
Ta có ![]()
![]()
![]()
Vật giá trị nhỏ nhất của biểu thức P là ![]()
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực R.
2. Phương trình vô nghiệm trên trường số phức C
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực
A. 0.
B. 1.
C. 3.
D. 2.
Chọn D.
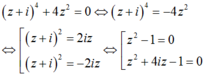
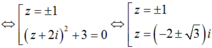
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn z - z 1 = 1 . Giá trị nhỏ nhất của P = z - z 2 là
A. 2016 - 1
B. 2017 - 1 2
C. 2016 - 1 2
D. 2017 - 1
Đáp án A
Phương pháp.
Giả sử ![]() Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa
Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa ![]() về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
Lời giải chi tiết.
Tính toán ta tìm được hai nghiệm 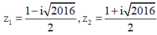
Giả sử ![]() . Từ
. Từ ![]() ta suy ra
ta suy ra
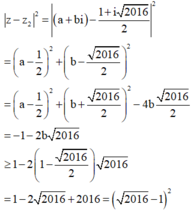
Áp dụng (1) ta nhận được
Do đó giá trị nhỏ nhất của ![]() là
2016
-
1
là
2016
-
1
Đạt được khi và chỉ khi ![]()
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn z - z 1 = 1 Giá trị nhỏ nhất của P = z - z 2 là
![]()
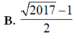
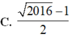
![]()
Trong tập các số phức gọi z 1 , z 2 là hai nghiệm của phương trình z 2 − z + 2017 4 = 0 với z 2 có phần ảo dương. Cho số phức z thỏa mãn z − z 1 = 1. Giá trị nhỏ nhất của P = z − z 2 là
A. 2016 − 1
B. 2017 − 1
C. 2017 − 1 2
D. 2016 − 1 2
Đáp án A
Phương trình z 2 − z + 2017 2 = 0 ⇔ 4 z 2 − 4 z + 2017 = 0
⇔ 2 z − 1 2 = 2016 i 2 ⇔ z 1 = 1 − i 2016 2 z 2 = 1 + i 2016 2
Ta có z − z 1 + z − z 2 ≥ z − z 1 − z − z 2 = z − z 2 ≥ z 1 − z 2 − z − z 1 = 2016 − 1
Vật giá trị nhỏ nhất của biểu thức P là P min = 2016 − 1
Trong tập các số phức, gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - z + 2017 4 = 0 với z 2 có thành phần ảo dương. Cho số phức z thỏa mãn | z - z 1 |=1 Giá trị nhỏ nhất của P=| z - z 2 |là
A. 2016 - 1
B. 2017 - 1 2
C. 2016 - 1 2
D. 2017 - 1