Có bao nhiêu mặt cầu tiếp xúc với cả 3 mặt phẳng tọa độ và có tâm thuộc (P): y - z - 4 0
Đọc tiếp
Có bao nhiêu mặt cầu tiếp xúc với cả 3 mặt phẳng tọa độ và có tâm thuộc (P): y - z - 4 = 0
Những câu hỏi liên quan
Có bao nhiêu mặt cầu tiếp xúc với cả 3 mặt phẳng tọa độ mà tâm của các mặt cầu đó đều thuộc mặt phẳng (P): y – z + 2 0?
Đọc tiếp
Có bao nhiêu mặt cầu tiếp xúc với cả 3 mặt phẳng tọa độ mà tâm của các mặt cầu đó đều thuộc mặt phẳng (P): y – z + 2 = 0?
Có bao nhiêu mặt cầu tiếp xúc với cả 3 mặt phẳng tọa độ và có tâm thuộc mặt phẳng
P
:
x
+
y
-
6
0
Đọc tiếp
Có bao nhiêu mặt cầu tiếp xúc với cả 3 mặt phẳng tọa độ và có tâm thuộc mặt phẳng P : x + y - 6 = 0
Cho
P
:
x
+
y
+
z
-
1
0
. Có bao nhiêu mặt cầu tiếp xúc với cả ba trục tọa độ và có tâm thuộc (P)?
Đọc tiếp
Cho P : x + y + z - 1 = 0 . Có bao nhiêu mặt cầu tiếp xúc với cả ba trục tọa độ và có tâm thuộc (P)?
Trong không gian với hệ tọa độ Oxyz, cho các mặt phẳng
P
:
2
x
−
y
−
z
−
2
0
;
Q
:
x
−
2
y
+
z
+
2
0
;
R
:
x
+
y
−
2
z
+
2
0
,...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các mặt phẳng P : 2 x − y − z − 2 = 0 ; Q : x − 2 y + z + 2 = 0 ; R : x + y − 2 z + 2 = 0 , T : x + y + z = 0 . Hỏi có bao nhiêu mặt cầu có tâm thuộc (T) và tiếp xúc với P , Q , R ?
A. 1
B. 2
C. 3
D. 4
Trong không gian với hệ tọa độ Oxy, cho các mặt phẳng
P
:
2
x
−
y
−
z
−
2
0
.
Q
:
x
−
2
y
+
z
+
2
0
;
R
:
x
+
y
−
2
z
+
2
0,...
Đọc tiếp
Trong không gian với hệ tọa độ Oxy, cho các mặt phẳng P : 2 x − y − z − 2 = 0 . Q : x − 2 y + z + 2 = 0 ; R : x + y − 2 z + 2 = 0, T : x + y + z = 0 . Hỏi có bao nhiêu mặt cầu có tâm thuộc (T) và tiếp xúc với P , Q , R ?
A.1
B.2
C.3
D.4
Đáp án D
Giả sử mặt cầu (S) có tâm I a ; b ; c ∈ T : a + b + c = 0
Theo bài ra d I ; P = d I ; Q = d I ; R
⇔ 2 a − b − c − 2 6 = a − 2 b + c + 2 6 = a + b − 2 c + 2 6
⇒ 3 a − 2 = 3 b − 2 3 a − 2 = 3 c − 2 a + b + c = 0 ⇒ a = b 3 a + 3 b = 4 a = c 3 a + 3 c = 4
M N // B A '
TH1: a + b + c = 0 a = b a = c ⇒ I 0 ; 0 ; 0
Tương tự cho các trường hợp còn lại
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai mặt cầu
P
:
x
2
+
y
2
+
z
2
+
4
x
+
2
y
+
z
0
và
Q
:
x
2
+
y
2
+
z
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt cầu P : x 2 + y 2 + z 2 + 4 x + 2 y + z = 0 và Q : x 2 + y 2 + z 2 − 2 x − y − z = 0 cắt nhau theo một đường tròn (C) và cho ba điểm A 1 ; 0 ; 0 , B 0 ; 1 ; 0 , C 0 ; 0 ; 1 . Hỏi có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng chứa đường tròn (C) và tiếp xúc với cả ba đường thẳng AB, AC, BC?
A. 4 mặt cầu
B. 1 mặt cầu
C. 2 mặt cầu
D. Vô số mặt cầu
Đáp án A
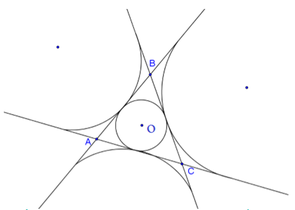
Ba điểm A,B,C tạo thành một tam giác. Có 4 đường tròn tiếp xúc với cả ba đường thẳng AB,AC,BC (hình vẽ trên).
Mặt cầu (S) cần tìm tiếp xúc với 3 đường thẳng AB,AC,BC, do đó nó phải chứa 1 trong 4 đường tròn trên.
Xét với 1 đường tròn bất kì trong 4 đường tròn trên, giả sử là đường tròn tâm (O) nằm bên trong tam giác, ta có:
Tâm I của mặt cầu (S) phải nằm trên đường thẳng d đi qua tâm O và vuông góc với (ABC). Mặt khác, I thuộc mp (P) chứa (C), (C) lại không vuông góc với (ABC) do đó chỉ có 1 giao điểm của d với (P). Tương tự, với 3 đường tròn còn lại, với mỗi đường tròn ta tìm được 1 tâm I nữa. Vậy có 4 mặt cầu thỏa mãn yêu cầu.
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz cho hai mặt cầu:
(
S
1
)
:
x
2
+
y
2
+
z
2
+
4
x
+
2
y
+
z
0
;
(
S
2
)
;
x
2...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho hai mặt cầu:
( S 1 ) : x 2 + y 2 + z 2 + 4 x + 2 y + z = 0 ;
( S 2 ) ; x 2 + y 2 + z 2 - 2 x - y - z = 0
cắt nhau theo một đường tròn (C) nằm trong mặt phẳng (P). Cho các điểm A (1; 0; 0), B (0; 2; 0), C (0; 0; 3). Có bao nhiêu mặt cầu tâm thuộc (P) và tiếp xúc với cả ba đường thẳng AB, BC, CA?
A. 4 Mặt cầu.
B. 2 Mặt cầu.
C. 3 Mặt cầu.
D. 1 Mặt cầu.
Chọn A
Mặt phẳng (P) chứa đường tròn (C) (giao của 2 mặt cầu đã cho) có phương trình là: 6x + 3y + 2z = 0
Mặt phẳng (P) có phương trình là:
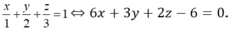
Do đó (P) // (ABC). Mặt cầu (S) tiếp xúc với cả ba đường thẳng AB, BC, CA sẽ giao với mặt phẳng (ABC) theo một đường tròn tiếp xúc với ba đường thẳng AB, BC, CA.
Trên mặt phẳng (ABC) có 4 đường tròn tiếp xúc với ba đường thẳng AB, BC, CA đó là đường tròn nội tiếp tam giác ABC và ba đường tròn bàng tiếp các góc A, B, C. Do đó có 4 mặt cầu có tâm nằm trên (P) và tiếp xúc với cả ba đường thẳng AB, BC, CA. Tâm của 4 mặt cầu là hình chiếu của tâm 4 đường tròn tiếp xúc với ba đường thẳng AB, BC, CA lên mặt phẳng (P).
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai mặt cầu:
S
1
x
2
+
y
2
+
z
2
+
4
x
+
2
y
+
z
0
,
S
2
x
2
+
y
2
+
z
2
-
2
x
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt cầu: S 1 = x 2 + y 2 + z 2 + 4 x + 2 y + z = 0 , S 2 = x 2 + y 2 + z 2 - 2 x - y - z = 0 cắt nhau theo một đường tròn (C) và ba điểm A 1 ; 0 ; 0 , B 0 ; 2 ; 0 và C 0 ; 0 ; 3 . Hỏi có tất cả bao nhiêu mặt cầu có tâm thuộc mặt phẳng chứa đường tròn (C) và tiếp xúc với ba đường thẳng AB, AC, BC
A. 1 mặt cầu
B. 2 mặt cầu
C. 4 mặt cầu.
D. Vô số mặt cầu.
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng
P
:
x
−
y
+
z
0
và mặt cầu (S) có tâm
I
1
;
−
1
;
1
và bán kính R 3. Từ một điểm M thuộc mặt phẳng (P) kẻ một đường thẳng tiếp xúc với mặt cầu S tại điểm N. Tính khoảng cách từ M tới gốc tọa độ biết rằng MN...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng P : x − y + z = 0 và mặt cầu (S) có tâm I 1 ; − 1 ; 1 và bán kính R = 3. Từ một điểm M thuộc mặt phẳng (P) kẻ một đường thẳng tiếp xúc với mặt cầu S tại điểm N. Tính khoảng cách từ M tới gốc tọa độ biết rằng MN = 4.
A. 19
B. 2 2
C. 22
D. 5
