Cho mặt phẳng (P): x-2y+z-4=0 và đường thẳng d : x - 3 3 = y + 5 - 5 = z - 3 - 1 . Viết phương trình hình chiếu vuông góc của d trên (P).
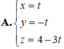
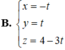
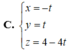
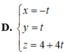
Cho mặt phẳng P : x - 2 y + z + 5 = 0 , Viết phương trình mặt phẳng (α) vuông góc với mặt phẳng (P) và chứa đường thẳng d là giao của hai mặt phẳng P 1 : x - 2 z = 0 và P 2 : 3 x - 2 y + z - 3 = 0
A. (α): 11x-2y-15z+3=0
B. (α): 11x+2y-15z-3=0
C. (α): 11x-2y+15z-3=0
D. (α): 11x-2y-15z-3=0
Chọn D
Từ phương trình hai mặt phẳng (P1), (P2) cho z = 1 ta tìm được điểm A(2;2;1) thuộc mặt phẳng (α) Tìm vecto chỉ phương của đường thẳng d. Vecto pháp tuyến của mặt phẳng cần tìm là tích có hướng của vecto pháp tuyến (P) và vecto chỉ phương của d
Cho mặt phẳng (P): x-2y+z+5=0. Viết phương trình mặt phẳng α vuông góc với mặt phẳng (P) và chứa đường thẳng d là giao của hai mặt phẳng P 1 : x - 2 z = 0 và P 2 : 3 x - 2 y + z - 3 = 0
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho đường thẳng d : x - 1 1 = y - 1 2 = z - 3 - 2 và mặt phẳng (P): 2x - 2y + z - 3 = 0, phương trình đường thẳng ∆ nằm trong mặt phẳng (P), cắt d và vuông góc với d là
A. x = 2 - 2 t y = 1 - 5 t z = - 5 - 6 t
B. x = - 2 - 2 t y = - 1 - 5 t z = 5 - 6 t
C. x = - 2 - 2 t y = - 1 + 5 t z = 5 - 8 t
D. x = - 2 - 2 t y = 1 - 5 t z = 5 + 6 t
Cho mặt phẳng P : x - 2 y + z - 4 = 0 và đường thẳng d : x - 3 3 = y + 5 - 5 = z - 3 - 1 . Viết phương trình hình chiếu vuông góc của d trên (P).
A. x = t y = - t z = 4 - 3 t
B. x = - t y = t z = 4 - 3 t
C. x = - t y = t z = 4 - 4 t
D. x = - t y = t z = 4 + 4 t
Chọn A
Tìm giao điểm I của d và (P). Hình chiếu vuông góc của đường thẳng qua điểm I và nhận vecto chỉ phương là tích có hướng của hai vecto: vecto pháp tuyến của mặt phẳng (P) và vecto pháp tuyến của mặt phẳng chứa d vuông góc với (P).
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng P : x + 2 y + z - 4 = 0 và đường thẳng d : x + 1 2 = y 1 = z + 2 3 . Viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d.
A. x - 1 5 = y - 1 - 1 = z - 1 - 3
B. x - 1 5 = y - 1 - 1 = z - 1 3
C. x - 1 5 = y - 1 1 = z - 1 - 3
D. x - 1 5 = y - 1 - 1 = z - 1 2
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng P : x + 2 y + z - 4 = 0 và đường thẳng d : x + 1 2 = y 1 = z + 2 3 .Viết phương trình đường thẳng ∆ nằm trong mặt phẳng P đồng thời cắt và vuông góc với đường thẳng d.
![]()
![]()
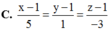
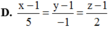
Đáp án A.
Ta có :
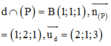
Do đường thẳng ∆ nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d tại B(1;1;1)
Mặt khác:
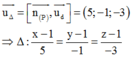
Trong không gian Oxyz, cho đường thẳng d có phương trình x + 1 1 = y - 1 2 = x - 3 - 2 và mặt phẳng (P) có phương trình 2x-2y+z-3=0. Tìm góc giữa d và mặt phẳng (P).
A. 63º
B. 35º
C. 55º
D. 27º
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình x+2y+z-4=0 và đường thẳng d: x + 1 2 = y 1 = z + 2 3 . Viết phương trình chính tắc của đường thẳng Δ nằm trong mặt phẳng (P), đồng thời cắt và vuông góc với đường thẳng d
A. x + 5 1 = y - 1 1 = z - 3 1
B. x - 5 1 = y + 1 1 = z + 3 1
C. x - 1 5 = y - 1 - 1 = z - 1 - 3
D. x + 1 5 = y + 1 - 1 = z + 1 - 3
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x+2y-z+5=0 và đường thẳng d : x + 3 2 = y + 1 1 = z - 3 1 Góc giữa đường thẳng (d) và mặt phẳng (P) là:
![]()
![]()
![]()
![]()