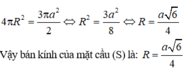Mặt cầu (S) có diện tích bằng 100 π c m 2 thì có bán kính là:
A. 3 cm
B. 5 cm .
C. 4 cm
D. 5 cm
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:
A. π ( a 2 + b 2 + c 2 ) B. 2 π ( a 2 + b 2 + c 2 )
C. 4 π ( a 2 + b 2 + c 2 ) D. π /2.( a 2 + b 2 + c 2 )
Chọn A.
Đường kính của mặt cầu (S) chính là đường chéo của hình hộp chữ nhật, nên mặt cầu (S) có bán kính
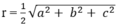
Do đó diện tích mặt cầu (S) là: S = 4 πr 2 = π( a 2 + b 2 + c 2 )
Cho mặt cầu (S) có bán kính R = 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu?
A. 32 3 ( c m 3 )
B. 60 3 ( c m 3 )
C. 20 3 ( c m 3 )
D. 96 3 ( c m 3 )
Cho khối cầu có diện tích S=8 π , thể tích V của khối cầu bằng:
![]()
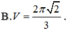
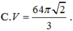
![]()
Một mặt cầu có diện tích xung quanh là π thì có bán kính bằng
A. 3 2
B. 3
C. 1 2
D. 1
Chọn C.
Phương pháp:
Công thức tính diện tích mặt cầu bán kính R là: S = 4 π R 2 .
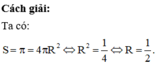
Một mặt cầu có diện tích xung quanh là π thì có bán kính bằng:
![]()
![]()
Cho hình cầu có diện tích mặt cầu là 64 π ( c m 2 ). Tính thể tích khối cầu?
A. 256 π 3 c m 3
B. 256 π c m 3
C. 64 π 3 c m 3
D. Đáp án khác
Mặt cầu (S) có diện tích bằng 20 π , thể tích khối cầu (S) bằng
A. 20 π 5 3
B. 20 π 5
C. 20 π 3
D. 4 π 5 3
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 là diện tích 6 mặt của hình lập phương, S 2 là diện tích xung quanh của hình trụ. Tỉ số S 2 / S 1 bằng:
A. π /6 B. 1/2
C. π /2 D. π
Trong không gian Oxyz, cho các điểm A(a;0;0), B(0;b;0), C(0;0;c) di động trên các trục Ox, Oy, Oz sao cho 2a+b-c-6=0 và hai điểm M(2;-3;5). Xét các mặt cầu (S) ngoại tiếp tứ diện OABC có tâm I. Khi 2 I M → + I N → đạt giá trị nhỏ nhất thì mặt cầu (S) có diện tích bằng
A. 14 π .
B. 64 π .
C. 56 π .
D. 16 π .
Cho hình vuông ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của AB và CD. Khi quay hình vuông ABCD quanh MN thành một hình trụ. Gọi (S) là mặt cầu có diện tích bằng diện tích toàn phần của hình trụ, tính có bán kính của mặt cầu (S)?
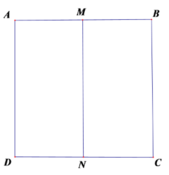
Mặt trụ tạo bởi hình vuông ABCD khi quay quanh MN có đường cao h = a và bán kính đáy ![]()
Diện tích 1 đáy và diện tích xung quanh của hình trụ là:
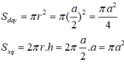
Nên có diện tích toàn phần của hình trụ:
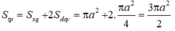
Mặt cầu (S) có bán kính R có diện tích bằng Stp của mặt trụ nên: