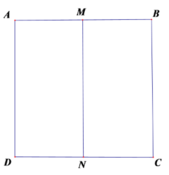
Mặt trụ tạo bởi hình vuông ABCD khi quay quanh MN có đường cao h = a và bán kính đáy ![]()
Diện tích 1 đáy và diện tích xung quanh của hình trụ là:
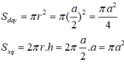
Nên có diện tích toàn phần của hình trụ:
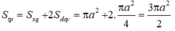
Mặt cầu (S) có bán kính R có diện tích bằng Stp của mặt trụ nên:
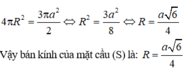

Mặt trụ tạo bởi hình vuông ABCD khi quay quanh MN có đường cao h = a và bán kính đáy ![]()
Diện tích 1 đáy và diện tích xung quanh của hình trụ là:
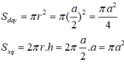
Nên có diện tích toàn phần của hình trụ:
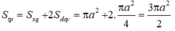
Mặt cầu (S) có bán kính R có diện tích bằng Stp của mặt trụ nên:
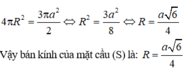
Cho hình chữ nhật ABCD có AB=a,
BC=2a. Gọi M,N lần lượt là trung điểm
của AB và CD. Thể tích của khối trụ tạo
thành khi quay hình chữ nhật ABCD
quanh trục MN bằng
![]()
![]()
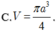
![]()
Trong không gian cho hình chữ nhật ABCD có AB=1, AD=2. Gọi M, N lần lượt là trung điểm AD và BC. Quay hình chữ nhật đó xung quanh trục MN ta được một hình trụ. Tính diện tích toàn phần của hình trụ đó?
![]()
![]()
![]()
![]()
Cho hình trụ (T) có bán kính đáy a trục
OO' bằng 2a và mặt cầu (S) có tâm là
trung điểm của đoạn thẳng OO' và đi
qua điểm O. Tìm tỉ số giữa diện tích
mặt cầu (S) và diện tích toàn phần của
hình trụ (T).
![]()
![]()
![]()
![]()
Trong không gian, cho hình chữ nhật ABCD có A B = 1 v à A D = 2 . Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần S t p của hình trụ đó.
A. S t p = 6 π
B. S t p = 2 π
C. S t p = 4 π
D. S t p = 10 π
Trong không gian, cho hình chữ nhật ABCD có AB=1 và AD=2. Gọi M,N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN , ta được một hình trụ. Tính diện tích toàn phần Stp của hình trụ đó.
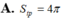
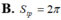
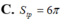
![]()
Một hình trụ có chiều cao h = 2 bán kính đáy r = 3.Một mặt phẳng (P) không vuông góc với đáy của hình trụ, lần lượt cắt hai đáy theo các đoạn giao tuyến AB và CD sao cho tứ giác ABCD là hình vuông. Tính diện tích S của hình vuông ABCD.
![]()
![]()
![]()
![]()
Cho hình trụ có bán kính r và có chiều cao cũng bằng r. Hình vuông ABCD có hai cạnh AB và CD lần lượt là các dây cung của hai đường tròn đáy, còn cạnh BC và AD không phải là đường sinh của hình trụ. Tính diện tích của hình vuông đó và côsin của góc giữa mặt phẳng chứa hình vuông và mặt phẳng đáy.
Trong không gian, cho hình thang cân ABCD có AB//CD, AB = a, CD = 2a, AD = a. Gọi M, N lần lượt là trung điểm của AB. CD. Gọi K là khối tròn xoay được tạo ra khi quay hình thành ABCD quanh trục MN. Tính diện tích toàn phần S t p của khối K.
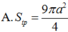
![]()
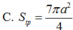
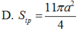
Cho mặt cầu (S) có bán kính R = a 3 . Gọi (T) là hình trụ có hai đường tròn đáy nằm trên (S) và diện tích thiết diện qua trục của hình trụ (T) là lớn nhất. Tính diện tích toàn phần S t p của (T)
A. S t p = 9 π a 2 .
B. S t p = 9 π a 2 3 .
C. S t p = 6 π a 2 3 .
D. S t p = 6 π a 2 .