Mạch dao động LC dao động điều hoà với tần số góc 1000 rad/s. Tại thời điểm t = 0 , dòng điện bằng 0. Thời điểm gần nhất mà năng lượng điện trường bằng 4 lần năng lượng từ trường là
A. 0,5 (ms)
B. 1,107 (ms)
C. 0,25 (ms)
D. 0,464 (ms)
Mạch dao động LC dao động điều hoà với tần số góc 1000 rad/s. Tại thời điểm t=0, dòng điện bằng 0. Thời điểm gần nhất mà năng lượng điện trường bằng 4 lần năng lượng từ trường là
A. 0,5 (ms)
B. 1,107 (ms)
C. 0,25 (ms)
D. 0,464 (ms)
Mạch dao động LC dao động điều hoà với tần số góc 1000 rad/s. Tại thời điểm t = 0 , dòng điện bằng 0. Thời điểm gần nhất mà năng lượng điện trường bằng 4 lần năng lượng từ trường là
A. 0,5 (ms)
B. 1,107 (ms)
C. 0,25 (ms)
D. 0,464 (ms)
Mạch dao động LC dao động điều hoà với tần số góc 1000 rad/s. Tại thời điểm t=0, dòng điện bằng 0. Thời điểm gần nhất mà năng lượng điện trường bằng 4 lần năng lượng từ trường là
A. 0,5 (ms)
B. 1,107 (ms)
C. 0,25 (ms)
D. 0,464 (ms)
Mạch dao động LC dao động điều hoà với tần số góc 1000 rad/s. Tại thời điểm t= 0, dòng điện bằng 0. Thời điểm gần nhất mà năng lượng điện trường bằng 4 lần năng lượng từ trường là
A. 0,5 (ms)
B. 1,107 (ms)
C. 0,25 (ms)
D. 0,464 (ms)
Chọn đáp án D
W C = 4 W L ⇒ W L = 1 5 W ⇒ i = 1 5 I 0 W C = 4 5 W
Thời gian ngắn nhất đi từ i= 0 đến i = 1 5 I 0 là arcsin:
t = 1 ω a r c cos i I 0 = 1 10 3 arcsin 1 5 ≈ 4,64.10 − 4 ( s )
Mạch dđ LC dđ điều hoà với tần số góc là 1000 rad/s. Tại thời điểm t=0, dòng điện bằng 0.Thời điểm gần nhất mà năng lượng điện trường bằng 4 lần năng lượng từ trường
\(W_{đt}=4W_{tt}\)\(\Leftrightarrow q=\frac{Q_0}{\sqrt{4+1}}=\frac{Q_0}{\sqrt{5}}\)\(\Rightarrow cos\varphi=\frac{1}{\sqrt{5}}\)\(\Rightarrow\varphi\approx63^o26'\)
\(\Rightarrow trong\) thời gian t: \(\varphi\Delta\approx26^033'\)
\(\Rightarrow t=\frac{T}{\frac{\Delta\varphi}{360}}=\frac{2\pi}{1000}\cdot\frac{800}{59}\approx0,0852s\)
Mạch dao động LC dao động điều hòa với tần số góc 1000 rad/s. Tại thời điểm t = 0, dòng điện bằng 0. Thời điểm gần nhất mà năng lượng điện trường bằng 4 lần năng lượng từ trường là:
Chu kì của dao động là:
\(T=\frac{2\pi}{\omega}=\frac{2\pi}{1000}=6,3.10^{-3}s\)
Vì tại t=0 i=0 nên thời điểm gần nhất mà năng lượng điện trường bằng 4 lần năng lượng từ trường khi góc \(\text{φ}=\frac{\pi}{6}\) .Thời gian để vật dao động đến vị trí góc
\(\text{φ }=\frac{\pi}{6}\)là:'
\(t=\frac{T}{12}=\frac{6,3.10^{-3}}{12}=5,25.10^{-4}s\)
Mạch dao động LC lí tưởng có tần số dao động là f = 10 4 3 H z . Tại tời điểm t=0 cường độ dòng điện trong mạch bằng không và đang giảm. Thời gian từ lúc mạch bắt đầu dao động đến lần thứ 2020 mà tại đó năng lượng điện từ gấp 4 lần năng lượng điện trường là
A. 0,15145s
B. 0,10075s
C. 0,30165s
D. 0,34685s
Đáp án A.
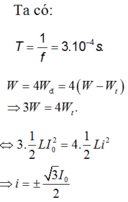
Trong 1 chu kì có 4 lần năng lượng điện từ gấp 4 lần năng lượng điện trường. Lần thứ 2020 ứng với chu kì thứ 2020 4 = 505 tức là sau 505 chu kì thì dòng điện trở lại trạng thái ban đầu (i=0, đang giảm).
Thời gian cần tìm là:
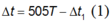
với ∆ t 1 : là thời gian dòng điện giảm từ i = 3 l 0 2 đến i=0, ứng với góc ở tâm mà bán kính quét được là:
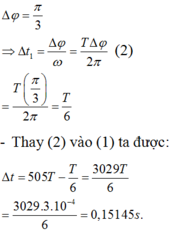
Một mạch dao động lí tưởng gồm cuộn cảm thuần L và tụ điện C thực hiện dao động điện từ tự do. Tại thời điểm t = 0 cường độ dòng điện trong mạch triệt tiêu. Tại thời điểm t = 150 μ s năng lượng điện trường và năng lượng từ trường trong mạch bằng nhau. Giá trị của tần số dao động của mạch gần giá trị nào nhất trong các giá trị sau. Biết tần số có giá trị từ 18kHz đến 20kHz.
A. 19523 Hz
B. 19654 Hz
C. 19166 Hz
D. 19782 Hz.
Đáp án C
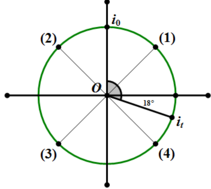
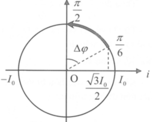
Tại thời điểm t = 0 thì i = 0 (vị trí i 0 trên hình vẽ)
Sau 2,7T thì có vị trí it như hình. Khoảng thời gian từ 2,7T đến 3T sẽ là góc i t O i 0 trên hình vẽ.
Để năng lượng điện trường và năng lượng từ trường bằng nhau thì:
![]()
Trong 1 chu kỳ sẽ có 4 lần đạt được trạng thái này ứng với 4 điểm 1,2,3,4 trên hình.
Như vậy ta thấy chỉ có điểm (1) là thỏa mãn NLĐT bằng NLTT và trong khoảng từ 2,7T đến 3T.
Dễ thấy từ i 0 đến (1) cần t = 2 T + 3 T 4 + T 8 = 2 , 875 T
![]()
Trong mạch dao động LC lí tưởng có dao động điện từ tự do với tần số 1 MHz. Tại thời điểm t = 0, năng lượng điện trường trong mạch có giá trị cực đại. Thời gian ngắn nhất kể từ thời điểm ban đầu để năng lượng điện trường bằng một nửa giá trị cực đại của nó là:
A. 2 . 10 - 6 s
B. 10 - 6 s
C. 0 , 5 . 10 - 6 s
D. 0 , 125 . 10 - 6 s
Đáp án D.

Tại thời điểm t = 0
w d = w d m a x ⇒ q 2 0 2 C = Q 2 0 2 C ⇒ q 0 = ± Q 0
khi w d = 1 2 w d m a x ⇒ q 2 2 C = 1 2 . Q 2 0 2 C ⇒ q = ± Q 0 2
Thời gian ngắn nhất là thời gian biến thiên từ Q 0 đến Q 0 / 2 , tương ứng với thời gian chuyển động từ B đến P (hình vẽ dưới đây), trong đó: OP = OB/ 2
Dễ thấy:
C o s M O P = O P O M = 1 2 ⇒ M O P = π 4 t = 45 0 360 0 T = 1 8 . 1 10 6 = 0 , 125 . 10 - 6 s