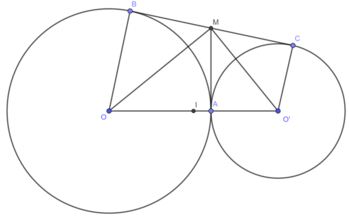
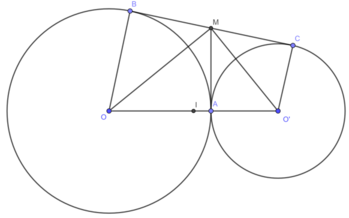
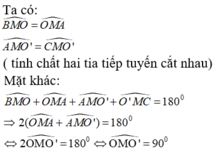Cho hai đường tròn (O) và (O’) cắt nhau ở A và B. Kẻ tiếp tuyến chung CD của hai đường tròn, C∈ (O); D ∈ (O’). Gọi I là giao điểm của AB và CD. Gọi E là điểm đối xứng với B qua I. Chứng minh rằng: a) BCED là hình bình hành b) Bốn điểm A, C, E , D thuộc cùng một đường tròn

Những câu hỏi liên quan
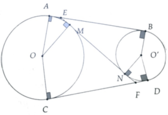
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại điểm A. Một tiếp tuyến của đường tròn (O) tại điểm B cắt (O’) tại C và D (C nằm giữa B và D). Các tia CA, DA cắt (O) tại E và F. a. Kẻ tiếp tuyến chung của hai đường tròn. Chứng minh rằng . b. Gọi M là điểm chính giữa của cung CD (M và A khác phía đối với CD). Chứng minh rằng .
Cho hai đường tròn (O; 16cm) và (O’; 9cm) tiếp xúc ngoài tại A. Gọi BC là tiếp tuyến chung ngoài của hai đường tròn (B ∈ (O), C ∈ (O')). Kẻ tiếp tuyến chung tại A cắt BC ở M. Tính độ dài BC
Ta có:
BM = MA
CM = MA
( tính chất hai tiếp tuyến cắt nhau)
⇒ BC = BM + MC = 2MA
Xét tam giác OMO’ vuông tại M có MA là đường cao.
Áp dụng hệ thức lượng trong tam giác vuông OMO’ có:
A M 2 = OM.O'M = 16.9 = 144 ⇒ AM = 12cm
⇒ BC = 2.12 = 24cm
Đúng 0
Bình luận (0)
Cho hai đường tròn (O; 16cm) và (O’; 9cm) tiếp xúc ngoài tại A. Gọi BC là tiếp tuyến chung ngoài của hai đường tròn (B ∈ (O), C ∈ (O')). Kẻ tiếp tuyến chung tại A cắt BC ở M. Tính góc OMO’
Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và CD (Ạ và C thuộc (O), B và D thuộc (O')). Tiếp tuyến chung trong MN cắt AB và CD theo thứ tự là E và F (M thuộc (O), N thuộc (O')). Chứng minh:
a, AB = EF
b, EM = FN
a, Ta có AB = AE + BE = EM + EN
Và CD = FD + FC = NF + NE
=> AB + CD = 2EF => AB = EF
b, Ta có EM = AB – EB = EF – EN = NF
Đúng 1
Bình luận (0)
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại điểm A. Một tiếp tuyếncủa đường tròn (O) tại điểm B cắt (O’) tại C và D (C nằm giữa B và D). Các tia CA, DA cắt(O) tại E và F.a. Kẻ tiếp tuyến chung xAx của hai đường tròn. Chứng minh rằng EF//CD .b. Gọi M là điểm chính giữa của cung CD (M và A khác phía đối với CD). Chứngminh rằng BAM90 độ .
Đọc tiếp
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại điểm A. Một tiếp tuyến
của đường tròn (O) tại điểm B cắt (O’) tại C và D (C nằm giữa B và D). Các tia CA, DA cắt
(O) tại E và F.
a. Kẻ tiếp tuyến chung xAx' của hai đường tròn. Chứng minh rằng EF//CD .
b. Gọi M là điểm chính giữa của cung CD (M và A khác phía đối với CD). Chứng
minh rằng BAM=90 độ .
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Kẻ tiếp tuyến chung CD (CD gần B hơn A) của hai đường tròn. C thuộc (O) và D thuộc (O’). Gọi I là giao điểm của AB và CD, E là điểm đối xứng với B qua I. Chứng minh rằng: B, C, E, D là 4 đỉnh của một hình bình hành.
Cho hai đường tròn (O; 16cm) và (O’; 9cm) tiếp xúc ngoài tại A. Gọi BC là tiếp tuyến chung ngoài của hai đường tròn (B ∈ (O), C ∈ (O')). Kẻ tiếp tuyến chung tại A cắt BC ở M. Gọi I là trung điểm của OO’. Chứng minh rằng BC là tiếp tuyến của đường tròn tâm I, bán kính IM.
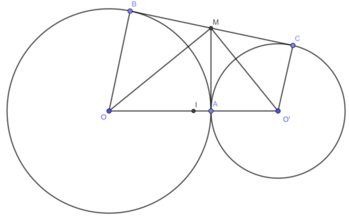
Ta có:
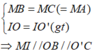
Mà OB ⊥ BC ⇒ IM ⊥ BC
Ta có:
IM ⊥ BC
BC ⋂ (I; IM) = {M}
Suy ra, BC là tiếp tuyến của đường tròn tâm I, bán kính IM
Đúng 0
Bình luận (0)
cho 2 đường tròn tâm O và tâm O' phân biệt. Hai đường tròn này cắt nhau tại 2 điểm A và B. Kẻ tiếp tuyến chung EF của hai đường tròn ( E thuộc (O), F thuộc (O')). gọi AB cắt EF tại C
Cho hai đường tròn (O,R)và (O`,r) tiếp xúc ngoài tại A kẻ tiếp tuyến chung ngoài DE của (O)và (O`), D€(O),E€(O')tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài DE ở I
a,tính số đo góc OIO'.
b, chứng minh OO' là tiếp tuyến của đường tròn đường kính DE
c, tính độ dài DE theo R và r
a: Xét (O) có
ID,IA là các tiếp tuyến
Do đó: IO là phân giác của góc DIA
=>\(\widehat{DIA}=2\cdot\widehat{OIA}\)
Xét (O') có
IA,IE là các tiếp tuyến
Do đó: IO' là phân giác của góc AIE
=>\(\widehat{AIE}=2\cdot\widehat{AIO'}\)
Ta có: \(\widehat{DIA}+\widehat{EIA}=180^0\)(hai góc kề bù)
=>\(2\left(\widehat{OIA}+\widehat{O'IA}\right)=180^0\)
=>\(2\cdot\widehat{OIO'}=180^0\)
=>\(\widehat{OIO'}=90^0\)
b: Xét (O) có
ID,IA là các tiếp tuyến
Do đó: ID=IA
Xét (O') có
IA,IE là các tiếp tuyến
Do đó: IA=IE
Ta có: IA=IE
ID=IA
Do đó: ID=IE
=>I là trung điểm của DE
=>I là tâm đường tròn đường kính DE
Xét ΔDAE có
AI là bán kính
\(AI=\dfrac{DE}{2}\)
Do đó: ΔADE vuông tại A
=>A nằm trên (I)
Xét (I) có
IA là bán kính
O'O\(\perp\)IA tại A
Do đó: OO' là tiếp tuyến của (I)
=>O'O là tiếp tuyến của đường tròn đường kính DE
Đúng 3
Bình luận (0)