Ta có:
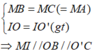
Mà OB ⊥ BC ⇒ IM ⊥ BC
Ta có:
IM ⊥ BC
BC ⋂ (I; IM) = {M}
Suy ra, BC là tiếp tuyến của đường tròn tâm I, bán kính IM

Ta có:
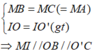
Mà OB ⊥ BC ⇒ IM ⊥ BC
Ta có:
IM ⊥ BC
BC ⋂ (I; IM) = {M}
Suy ra, BC là tiếp tuyến của đường tròn tâm I, bán kính IM
Cho hai đường tròn (O; 16cm) và (O’; 9cm) tiếp xúc ngoài tại A. Gọi BC là tiếp tuyến chung ngoài của hai đường tròn (B ∈ (O), C ∈ (O')). Kẻ tiếp tuyến chung tại A cắt BC ở M. Tính độ dài BC
Cho hai đường tròn (O; 16cm) và (O’; 9cm) tiếp xúc ngoài tại A. Gọi BC là tiếp tuyến chung ngoài của hai đường tròn (B ∈ (O), C ∈ (O')). Kẻ tiếp tuyến chung tại A cắt BC ở M. Tính góc OMO’
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài, B ∈ (O), C ∈ (O'). Tiếp tuyến chung trong tại A cắt BC ở điểm M. Gọi E là giao điểm của OM và AB, F là giao điểm của O'M và AC. Chứng minh rằng:
OO' là tiếp tuyến của đường tròn có đường kính là BC
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài, B ∈ (O), C ∈ (O'). Tiếp tuyến chung trong tại A cắt BC ở điểm M. Gọi E là giao điểm của OM và AB, F là giao điểm của O'M và AC. Chứng minh rằng:
BC là tiếp tuyến của đường tròn có đường kính OO'
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài, B thuộc (O), C thuộc(O').Tiếp tuyến chung trong tại A cắt BC ở điểm M. Gọi E là giao điểm của OM và AB, F là giao điểm của O'M và AC. Chứng minh rằng :
a/ Tứ giác AEMF là hình chữ nhật
b/ ME*MO=MF*MO'
c/ OO' là tiếp tuyến của đường tròn có đường kính là BC.
d/ BC là tiếp tuyến của đường tròn có đường kính là OO'
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài DE, D ∈ (O), E ∈ (O’). Kẻ tiếp tuyến chung trong tại A cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O’I và AE. Chứng minh rằng OO’ là tiếp tuyến của đường tròn có đường kính là DE
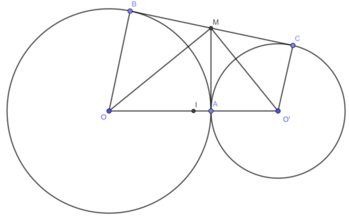
Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài với nhau tại A. Vẽ tiếp tuyến chung ngoài BC với B ∈ (O), C ∈ (O'). Đường vuông góc với OO' kẻ từ A cắt BC ở M
a, Tính MA theo R và r
b, Tính diện tích tứ giác BCO'O theo R và r
c, Tính diện tích ∆BAC theo R và r
d, Gọi I là trung điểm của OO'. Chứng minh rằng BC là tiếp tuyến của đường tròn (I; IM)
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Vẽ tiếp tuyến chung ngoài BC với \(B\in\left(O\right)\)và \(C\in\left(O'\right)\). Tiếp tuyến chung tại A cắt BC tại M.
a) Số đo góc BAC ?
b) Từ M kẻ MO cắt AB tại H, MO' cắt AC tại K. CM: HK = MA
c) Gọi I là trung điểm OO'. CM: BC là tiếp tuyến của đường tròn tâm I đường kính OO'
Cho đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC với B ∈ (O), C ∈ (O’). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC ở I
a, Vẽ đường kính BOD và CO'E. Chứng mình các bộ ba điểm B,A, E và C, A, D thẳng hàng
b, Chứng minh ∆BAC và ∆DAE có diện tích bằng nhau
c, Gọi K là trung điểm của DE. Chứng minh đường tròn ngoại tiếp ∆OKO' tiếp xúc với BC