Cho các số thực a, b thảo mãn 0 < a < 1 < b . Tìm khẳng định đúng:
![]()
![]()
![]()
![]()
Cho các số thực a, b thỏa mãn 0 < a < 1 < b . Tìm khẳng định đúng:
A. log a b < 0
B. ln a > ln b
C. 0 , 5 a < 0 , 5 b
D. 2 a > 2 b .
Chọn A.
Phương pháp
Xét tính đúng sai của từng đáp án dựa vào điểu kiện của a, b.
Cách giải:
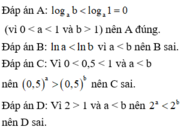
Cho các số thực a, b thỏa mãn 0<a<b. Khẳng định nào sau đây đúng?
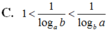
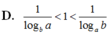
Cho a, b, c là các số thực thỏa mãn 0 < a ≠ 1 v à b c > 0 . Trong các khẳng định sau:
I . log a b c = log a b + log a c I I . log a b c = 1 log b c a I I I . log a b c 2 = 2 log a b c I V . log a b 4 = 4 log a b
Có bao nhiêu khẳng định đúng?
A. 0
B. 1
C. 2
D. 3
Cho a,b,c là các số thực thỏa mãn 0 < a ≠ 1 v à b c > 0. Trong các khẳng định sau:
I . log a b c = log a b + l o g a c
I I . log a b c = log a b − l o g a c
I I I . log a b c 2 = 2 log a b c
I V . log a b 4 = 4 log a b
Có bao nhiêu khẳng định đúng
A.2
B.3
C.1
D.0
Đáp án C
Ta có sai vì chưa có điều kiện b > 0 ; c > 0 . Vậy khẳng định đúng.
Cho a , b , c là số thực thỏa mãn 0 < a ≠ 1 và b c > 0. Trong các khẳng định sau:
I. log a b c = log a b + log a c .
II. log a b c = 1 log b c a .
III. log a b c 2 = 2 log a b c .
IV. log a b 4 = 4 log a b .
Có bao nhiêu khẳng định đúng?
A. 0.
B. 1.
C. 2.
D. 3.
Cho a, b là hai số thực thoả mãn 0 < a < 1 < b khẳng định nào sau đây đúng?
A. l o g b a + l o g a b < 0 .
B. l o g b a > 1 .
C. l o g a b > 0 .
D. l o g b a + l o g a b ≥ 0 .
Cho a, b là các số thực dương thỏa mãn log 2 a + log 2 b = 0. Khẳng định nào sau đây đúng?
A. a + b = 2
B. a + b = 1
C. ab=1
D. ab=2
Cho 2 số thực dương a,b thỏa mãn 1> a> b> 0 Khẳng định nào sau đây là đúng
A. logab< 1< logba
B. 1< logab< log ba
C. logab< logba< 1
D. logba< 1< logab
Chọn D
Cho 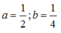 ta thấy logab= 2 và logba= ½. Do vậy logba< 1< logab
ta thấy logab= 2 và logba= ½. Do vậy logba< 1< logab
Cho các số thực a, b thỏa mãn 1 < a < b . Khẳng định nào sau đây đúng?
A. 1 log a b < 1 < 1 log b a
B. 1 log a b < 1 log b a < 1
C. 1 < 1 log a b < 1 log b a
D. 1 log b a < 1 < 1 log a b
Đáp án A
Phương pháp:
log a x < log a y ⇔ a > 1 0 < x < y 0 < a < 1 x > y > 0
Cách giải:
Ta có:
1 < a < b ⇒ 1 = log a a < log a b log b a < log b b = 1 ⇒ log b a < 1 < log a b ⇒ 1 log a b < 1 < 1 log b a