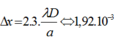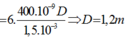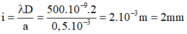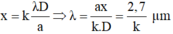Trong thí nghiệm Y âng về giao thoa ánh sáng, khoảng cách giữa hai khe sáng là 1,5mm. khi chiếu vào hai khe chùm bức xạ có bước sóng γ = 400 n m thì hai vân sáng bậc 3 cách nhau 1,92mm. Khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là:
A. 1,2 m
B. 2,4 m
C. 1,8 m
D. 3,6 m